题目内容
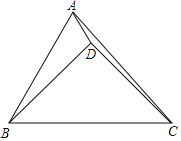
【题目】如图,△ABC中,∠ABC=60°,BC=8,点D为△ABC内一点,BD=CD,∠ABD+∠ADC=180°,若AD=2,则AC的长为_____.
【答案】2![]()
【解析】
延长AD交BC于E,在AB上截取AF=AD,连接DF,作AH⊥BC于H,设∠ABD=α,先根据角度之间的转化得出∠BAD=60°,从而得出△ABE为等边三角形,进而得出△ADF也为等边三角形.利用SAS证明△BFD≌△DEC,得出EC=DF=AD,然后可求出BE的长,在等边△ABE中,根据勾股定理可得出AH的长,最后在Rt△ACH中,利用勾股定理可得出AC的长.
解:如图,延长AD交BC于E,在AB上截取AF=AD,连接DF,作AH⊥BC于H.

设∠ABD=α,则∠ADC=180°﹣α,∠DBC=60°﹣α,∠EDC=α,
∵DB=DC,
∴∠DCB=∠DBC=60°﹣α,
∴∠BDC=60°+2α,
∴∠BDE=∠BDC-∠EDC=60°+α,
又∠BDE=∠ABD+∠BAE=α+∠BAE,
∴∠BAE=60°,又∠ABE=60°,
∴△AEB是等边三角形,
∵AF=AD=2,
∴△ADF是等边三角形,
∴DF=AD=AF=2,
∵∠FBD=∠EDC=α,BF=DE,BD=DC,
∴△BFD≌△DEC(SAS),
∴EC=DF=2,
∵BC=8,
∴BE=AB=AE=8﹣2=6,
∵AH⊥EB,
∴BH=EH=3,
∴AH=![]() =
=![]() =3
=3![]() ,
,
又CH=CE+EH=2+3=5,
∴AC=![]() =
=![]() =2
=2![]() .
.
故答案为:2![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目