题目内容
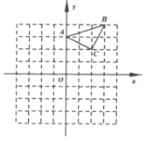
【题目】如图,在△ABC中,AB=AC=5,BC=6,点M在△ABC内,AM平分∠BAC.点E与点M在AC所在直线的两侧,AE⊥AB,AE=BC,点N在AC边上,CN=AM,连接ME,BN.
(1)补全图形;
(2)求ME:BN的值;
(3)问:点M在何处时BM+BN取得最小值?确定此时点M的位置,并求此时BM+BN的最小值.
【答案】(1)补图见解析;(2)ME:BN=1;(3)当点M在∠BAC的平分线上运动到它与BE的交点处时,BM+BN取得最小值,为![]() .
.
【解析】
(1)根据题意补全图形;
(2)延长AM交BC于点D,证明△AME≌△CNB,根据全等三角形的性质得到ME=BN,得到答案;
(3)根据ME=BN,得到BM+BN=BM+ME,根据两点之间线段最短、勾股定理计算即可.
(1)补全图形见图1:
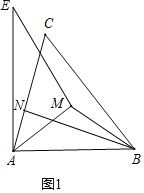
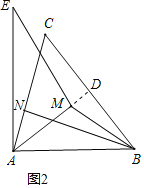
(2)如图2,延长AM交BC于点D,
∵AB=AC,AM平分∠BAC,
∴∠CAD=∠BAD,AD⊥BC,
∵AE⊥AB,
∴∠MAE+∠BAD=90°,
∵AD⊥BC,
∴∠C+∠CAD=90°,
∴∠MAE=∠C,
在△AME和△CNB中,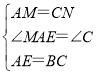 ,
,
∴△AME≌△CNB(SAS),
∴ME=BN,
∴ME:BN=1;
(3)∵ME=BN,
∴BM+BN=BM+ME,
∴当点M在∠BAC的平分线上运动到它与BE的交点处时,BM+BN取得最小值,
∵AB=AC=5,BC=6,
∴AE=BC=6,
∴BE=![]() ,
,
∴BM+BN的最小值为![]() .
.

练习册系列答案
相关题目