题目内容
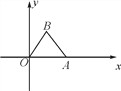
【题目】如图,△OAB的OA边在x轴上,其中B点坐标为(3,4)且OB=BA.
(1)求经过A,B,O三点的抛物线的解析式;
(2)将(1)中的抛物线沿x轴平移,设点A,B的对应点分别为点A′,B′,若四边形ABB′A′为菱形,求平移后的抛物线的解析式.
【答案】(1) y=-![]() x2+
x2+![]() x (2)①y=-
x (2)①y=-![]() (x-8)2+4;②y=-
(x-8)2+4;②y=-![]() (x+2)2+4
(x+2)2+4
【解析】试题分析:(1)根据题意,利用待定系数发求解即可;
(2)先根据菱形的性质,结合勾股定理求出菱形的边长,然后根据二次函数的平移得到函数的解析式.
试题解析:(1)设所求抛物线的解析式为y=ax(x-6),将(3,4)代入,可得4=-9a,∴a=-![]() ,∴y=-
,∴y=-![]() x(x-6)=-
x(x-6)=-![]() x2+
x2+![]() x (2)∵B(3,4),A(6,0),∴BA=
x (2)∵B(3,4),A(6,0),∴BA=![]() =5.∵四边形ABB′A′为菱形,∴BB′=BA=5.①若抛物线沿x轴向右平移,则B′(8,4),∴平移后抛物线的解析式为y=-
=5.∵四边形ABB′A′为菱形,∴BB′=BA=5.①若抛物线沿x轴向右平移,则B′(8,4),∴平移后抛物线的解析式为y=-![]() (x-8)2+4;②若抛物线沿x轴向左平移,则B′(-2,4),∴平移后抛物线的解析式为y=
(x-8)2+4;②若抛物线沿x轴向左平移,则B′(-2,4),∴平移后抛物线的解析式为y=![]() (x+2)2+4
(x+2)2+4

练习册系列答案
相关题目