题目内容
【题目】如图,四边形ABCD内接于⊙O,AC平分∠BAD,延长DC交AB的延长线于点E .
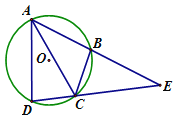
(1)若∠ADC=86°,求∠CBE的度数;
(2)若AC=EC,求证:AD=BE.
【答案】(1) ∠CBE=86°;(2)证明见解析.
【解析】试题分析:(1)根据圆内接四边形的性质计算即可;(2)证明△ADC≌△EBC即可.
试题解析:(1) ∵ 四边形ABCD内接于⊙O,
∴ ∠ADC+ ∠ABC= 180°.
又∵ ∠ADC= 86°,
∴ ∠ABC= 94°,
∴ ∠CBE=180° - 94°=86°.
(2)∵ AC=EC,
∴ ∠E=∠CAE ,
∵ AC平分∠BAD,
∴ ∠DAC=∠CAB ,
∴ ∠DAC= ∠E.
∵ 四边形ABCD内接于⊙O,
∴ ∠ADC+ ∠ABC= 180°,
又∵∠CBE+∠ABC = 180°, ,
∴ ∠ADC= ∠CBE,
∴ △ADC ≌ △EBC ,
∴ AD=BE .

练习册系列答案
相关题目