题目内容
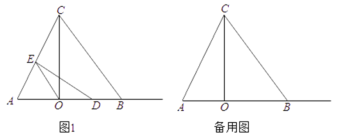
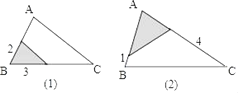
【题目】如图1,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
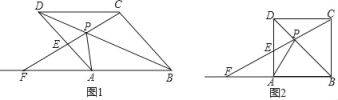
(1)求证:△APD≌△CPD;
(2)如图2,当菱形ABCD变为正方形,且PC=2,tan∠PFA=![]() 时,求正方形ABCD的边长.
时,求正方形ABCD的边长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据菱形的性质得:AD=CD,∠ADP=∠CDP,根据SAS即可证明△APD≌△CPD;
(2)先根据tan∠PFA![]() ,设BC=a,则BF=2a,证明△DPC∽△BPF,得
,设BC=a,则BF=2a,证明△DPC∽△BPF,得![]() ,求FC=6,根据勾股定理列方程得:62=a2+(2a)2,可得正方形ABCD的边长.
,求FC=6,根据勾股定理列方程得:62=a2+(2a)2,可得正方形ABCD的边长.
(1)∵四边形ABCD是菱形,∴AD=CD,∠ADP=∠CDP.
在△APD和△CPD中,∵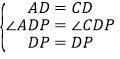 ,∴△APD≌△CPD(SAS);
,∴△APD≌△CPD(SAS);
(2)∵四边形ABCD是正方形,∴∠ABC=90°,CD=BC.
∵tan∠PFA![]() ,设BC=a,则BF=2a.
,设BC=a,则BF=2a.
∵DC=BC=a,DC∥BF,∴∠DCP=∠PFB,∠CDP=∠PBF,∴△DPC∽△BPF,∴![]() .
.
∵PC=2,∴PF=4,∴FC=PC+PF=6.
在Rt△FCB中,FC2=BC2+FB2,∴62=a2+(2a)2,解得:a![]() 或
或![]() (舍),∴正方形ABCD的边长为
(舍),∴正方形ABCD的边长为![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目