题目内容
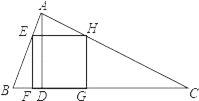
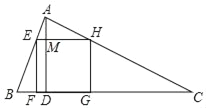
【题目】如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E，H分别在AB，AC上，已知BC=40cm，AD=30cm，求这个正方形的边长．
【答案】
【解析】
根据EH∥BC得出△AEH∽△ABC，设AD与EH交于点M，证明四边形EFDM是矩形，设正方形边长为x，再利用△AEH∽△ABC，得
，列出方程即可解决问题．
∵四边形EFGH是正方形，
∴EH∥BC，
∴∠AEH=∠B，∠AHE=∠C，
∴△AEH∽△ABC．
如图，设AD与EH交于点M．
∵∠EFD=∠FEM=∠FDM=90°，
∴四边形EFDM是矩形，
∴EF=DM，设正方形EFGH的边长为xcm，
∵△AEH∽△ABC，
∴，
∴
，
∴x=，
∴正方形EFGH的边长为cm．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
