Question

【题目】如图，Rt△ABC中，∠BAC=90°，AB=6，sinC=，以点A为圆心，AB长为半径作弧交AC于M，分别以B、M为圆心，以大于BM长为半径作弧，两弧相交于点N，射线AN与BC相交于D，则AD的长为_____．

Answer 1

【答案】

【解析】

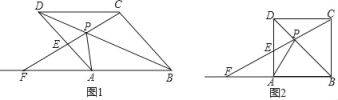
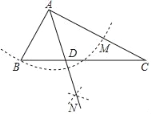
过D作DE⊥AB于E，DF⊥AC于F，设AE=DE=AF=DF=x，则BE=6﹣x，CF=8﹣x，依据∠B=∠FDC，∠BDE=∠C，可得△BDE∽△DCF，依据相似三角形对应边成比例，即可得到AE的长，进而得出AD的长．

如图，过D作DE⊥AB于E，DF⊥AC于F，由题可得：AD平分∠BAC，∠BAC=90°，∴四边形AEDF是正方形，∴DE=DF，∠BAD=45°=∠ADE，∴AE=DE=AF=DF．

∵∠BAC=90°，AB=6，sinC，∴BC=10，AC=8，设AE=DE=AF=DF=x，则BE=6﹣x，CF=8﹣x．

∵∠B=∠FDC，∠BDE=∠C，∴△BDE∽△DCF，∴，即，解得：x，∴AE，∴Rt△ADE中，ADAE．

故答案为：．