Question

【题目】如图，半径为1的半圆形纸片，按如图方式折叠，使对折后圆弧的中点M与圆心O重合，则图中阴影部分的面积是.

Answer 1

【答案】
【解析】解：如图，连接OM，交弦AB于C，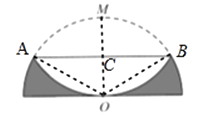

由题意知，OM⊥AB，且OC=MC= ，
在Rt△AOC中，∵OA=1，OC= ，
∴cos∠AOC= = ，AC= = ，
∴∠AOC=60°，AB=2AC= ，
∴∠AOB=2∠AOC=120°，
则S弓形ABM=S扇形OAB-S△AOB= - × × = ，
则S阴影= S半圆-2S弓形ABM= π×12-2（ ）= .
故答案为 .
分割图形可知阴影部分的面积就等于S半圆-2S弓形ABM ， 圆的半径已知，则只需要求出S弓形ABM=S扇形OAB-S△AOB ， 要S扇形OAB的面积，则必要求出圆心角∠AOB，则∠AOC必是特殊角；根据折叠可得OC=MC，且OM⊥AB，由垂径定理可得AC=BC，在Rt△AOC中，OA=1，OC= ，则可得∠AOC=60°，及AC的边长，即可解答.