题目内容
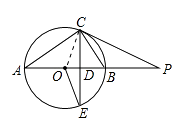
【题目】如图，AB是⊙O的直径，点P在AB的延长线上，弦CE交AB于点D．连接OE、AC，且∠P=∠E，∠POE=2∠CAB．
（1）求证：CE⊥AB；
（2）求证：PC是⊙O的切线；
（3）若BD=2OD，PB=9，求⊙O的半径及tan∠P的值．
【答案】
（1）
证明：连接OC，
∴∠COB=2∠CAB，
又∠POE=2∠CAB．
∴∠COD=∠EOD，
则弧BC=弧BE，
即CE⊥AB；
（2）
证明：∵CE⊥AB，∠P=∠E，
∴∠P+∠PCD=∠E+∠PCD=90°，
又∠OCD=∠E，
∴∠OCD+∠PCD=∠PCO=90°，
∴PC是⊙O的切线；
（3）
解：设⊙O的半径为r，OD=x，则BD=2x，r=3x，
∵CD⊥OP，OC⊥PC，
∴Rt△OCD∽Rt△OPC，
∴OC2=ODOP，即（3x）2=x（3x+9），
解之得x= 
，
∴⊙O的半径r= 
，
在Rt△OCP中， PC= 
= 
=9 
，
tan∠P= 
= 
.
【解析】（1）此题方法不唯一，主要是运用“同弧所对的圆周角是圆心角的一半”，题中给出的是证明弧BC和弧BE所对的圆心角相等，则所对的弧相等，则由垂径定理可证得；
2）证明相切，需证明半径OC⊥CP，即证明∠PCO=90°；而由（1）可得∠P+∠PCD=∠E+∠PCD=90°，而由半径OE=OC，根据等边对等角，可得∠OCD=∠E，则可证得∠OCD+∠PCD=∠PCO=90°；
3）要求⊙O的半径，可考虑运用勾股定理的方法和相似三角形的方法，题中给出的是运用相似三角形的判定和性质解答，由BD=2OD，可得边BD，半径与OD的关系，则证明Rt△OCD∽Rt△OPC，可得边 OC2=ODOP，代入相关数据，求出半径OC和OD；在Rt△OCP中，tan∠P= ，OC已求，则PO=OB+PB，则可求出PC，代入即可解出.
【考点精析】关于本题考查的勾股定理的概念和切线的性质定理，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案．
