��Ŀ����
����Ŀ����ѧ�����ת�任
��1����ͼ�٣��ڡ�ABC�У���ABC=130�㣬����ABC�Ƶ�C��ʱ����ת50��õ���A��B��C������BB�䣬���A��B��B�Ĵ�С��
��2����ͼ�ڣ��ڡ�ABC�У���ABC=150�㣬AB=3��BC=5������ABC�Ƶ�C��ʱ����ת60��õ���A��B��C������BB�䣬��A��ΪԲ�ģ�A��B�䳤Ϊ�뾶��Բ��
�ٲ��룺ֱ��BB�����A���λ�ù�ϵ����֤����Ľ��ۣ�
������A��B�����߶�A��B�ij��ȣ�
��3����ͼ�ۣ��ڡ�ABC�У���ABC=����90�㣼����180�㣩��AB=m��BC=n������ABC�Ƶ�C��ʱ����ת2�½Ƕȣ�0�㣼2�£�180�㣩�õ���A��B��C������A��B��BB�䣬��A��ΪԲ�ģ�A��B�䳤Ϊ�뾶��Բ���ʣ��Ǧ���Ǧ�����ʲô����ʱ��ֱ��BB�����A�����У���˵�����ɣ�������������߶�A��B�ij��ȣ�����ýǦ���Ǧµ����Ǻ�������ĸm��n����ɵ�ʽ�ӱ�ʾ��
���𰸡�
��1��
�⣺��ͼ����
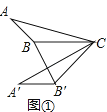 ��
��
�ߡ�A��B��C���ɡ�ABC��ת�õ���
���A��B��C=��ABC=130�㣬CB=CB�䣬
���CBB��=��CB��B���ߡ�BCB��=50�㣬
���CBB��=��CB��B=65�㣬
���A��B��B=��A��B��C����BB��C=65��
��2��
�⣺�ٽ��ۣ�ֱ��BB�䡢�ǡ�A������ߣ����ɣ���ͼ����
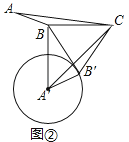 ��
��
�ߡ�A��B��C=��ABC=150�㣬CB=CB�䣬
���CBB��=��CB��B���ߡ�BCB��=60�㣬
���CBB��=��CB��B=60�㣬
���A��B��B=��A��B��C����BB��C=90�㣮
��AB���BB�䣬
��ֱ��BB�䡢�ǡ�A������ߣ�
�ڡ���RT��ABB���У��ߡ�AB��B=90�㣬BB��=BC=5��AB��=AB=3��
��A��B= ![]() =
= ![]()
��3��
�⣺��ͼ����
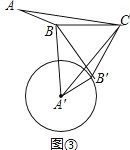 ��
��
����+��=180��ʱ��ֱ��BB�䡢�ǡ�A������ߣ�
���ɣ��ߡ�A��B��C=��ABC=����CB=CB�䣬
���CBB��=��CB��B���ߡ�BCB��=2�£�
���CBB��=��CB��B= ![]() ��
��
���A��B��B=��A��B��C����BB��C=����90��+��=180�㩁90��=90�㣮
��AB���BB�䣬
��ֱ��BB�䡢�ǡ�A������ߣ�
�ڡ�CBB���С�CB=CB��=n����BCB��=2�£�
��BB��=2nsin�£�
��RT��A��BB����A��B= ![]()
����������1�����ݡ�A��B��B=��A��B��C����BB��C��ֻҪ�����A��B��B���ɣ���2�������ۣ�ֱ��BB�䡢�ǡ�A������ߣ�ֻҪ֤����A��B��B=90�㼴�ɣ�������RT��ABB���У����ù��ɶ������㼴�ɣ���3����ͼ���У�����+��=180��ʱ��ֱ��BB�䡢�ǡ�A������ߣ�ֻҪ֤����A��B��B=90�㼴�ɽ�����⣮�ڡ�CBB�������BB�䣬����RT��A��B��B�����ù��ɶ������ɣ����⿼��Բ���ۺ��⡢��ת�����ԡ����ɶ��������ߵ��ж������������ε����ʵ�֪ʶ������Ĺؼ�������������Щ֪ʶ������⣬���������ת�����ԣ������п�ѹ���⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�





