题目内容
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() ,
,![]() 是
是![]() 上两点,且
上两点,且![]() ,连接
,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,垂足为
,垂足为![]() .
.
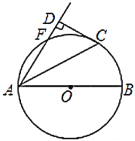
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)见解析;(2)圆O 的半径为8
【解析】
(1)连结OC,由![]() 根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
(2)连结BC,由AB为直径得∠ACB=90°,由![]() 得∠BOC=60°,则∠BAC=30°,所以∠DAC=30°,在Rt△ADC中,利用含30度的直角三角形三边的关系得
得∠BOC=60°,则∠BAC=30°,所以∠DAC=30°,在Rt△ADC中,利用含30度的直角三角形三边的关系得![]() ,在Rt△ACB中,利用含30度的直角三角形三边的关系得
,在Rt△ACB中,利用含30度的直角三角形三边的关系得![]() AB=2BC=8,从而求出⊙O的半径.
AB=2BC=8,从而求出⊙O的半径.
解:(1)证明:连结OC,如图
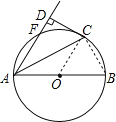
∵弧FC=弧BC
∴∠FAC=∠BAC,
∵OA=OC,∴∠OAC=∠OCA,
∴∠FAC=∠OCA,∴0C // AF,
∵CD⊥AF,∴0C⊥CD,
∴CD是圆O的切线;
(2)连结BC,如图,
∵AB为直径,
∴∠ACB=90°,∵![]() ,
,
∴∠BOC= ![]() ×180°=60°,∴∠BAC=30,
×180°=60°,∴∠BAC=30,
∴∠DAC=30,在RtΔADC中,CD=![]() ,
,
∴AC=2CD=![]() ,在RtΔACB中,BC=
,在RtΔACB中,BC=![]() AC=
AC=![]() =8,
=8,
∴AB=2BC=16,∴圆O 的半径为8.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目