Question

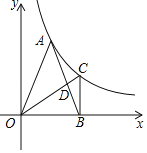
【题目】在平面直角坐标系中，抛物线y＝﹣（x﹣m）2+4（m＞0）的顶点为A，与直线x＝相交于点B，点A关于直线x＝的对称点为C．

（1）若抛物线y＝﹣（x﹣m）2+4（m＞0）经过原点，求m的值．

（2）点C的坐标为　 　．用含m的代数式表示点B到直线AC的距离为　 　．

（3）将y＝﹣（x﹣m）2+4（m＞0，且x≥）的函数图象记为图象G，图象G关于直线x＝的对称图象记为图象H．图象G与图象H组合成的图象记为图象M．

①当图象M与x轴恰好有三个交点时，求m的值．

②当△ABC为等腰直角三角形时，直接写出图象M所对应的函数值小于0时，自变量x的取值范围．

Answer 1

【答案】（1）m＝2．（2）（0，4），；（3）①m＝4，②x＜﹣2或x＞4．

【解析】

(1)将原点坐标代入解出即可.

(2)根据顶点公式算出C点坐标即可,算出AC的解析式,再求出B到AC的距离.

(3)①画出图象即可看出B的坐标,列式计算即可;②分别表示出A、B、C的坐标,令BE=AE代入算出结果.

（1）∵抛物线y＝﹣（x﹣m）2+4（m＞0）经过原点，

∴0＝﹣（0﹣m）2+4，

解得 m1＝2，m2＝﹣2，

∵m＞0，

∴m＝2．

（2）∵抛物线y＝﹣（x﹣m）2+4（m＞0），

∴顶点A坐标为（m，4），

∵点A关于直线x＝的对称点为C．

∴点C的坐标为（0，4）；

∴直线AC解析式为y＝4，

当x＝时，y＝﹣+4，

∴点B（，﹣+4），

∴点B到直线AC的距离为，

故答案为：（0，4），；

（3）①如图，当图象M与x轴恰好有三个交点时，

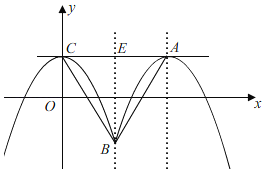
∴点 B在x轴上，且点B（，﹣+4），

∴0＝﹣+4

∴m1＝4，m2＝﹣4（舍去）

②∵△ABC为等腰直角三角形，

∴BE＝CE＝AE＝AC，

∵B（，﹣+4），A（m，2），C（0，2），（m＞0）

∴BE＝，AE＝||＝，

∴＝

∴m1＝2，m2＝0（不合题意舍去），

∴抛物线解析式为：y＝﹣（x﹣2）2+4，

当y＝0时，0＝﹣（x﹣2）2+4，

∴x1＝0＜＝1（不合题意舍去），x2＝4，

∴图象G与x轴的交点为（4，0），且图象G关于直线x＝的对称图象记为图象H．

∴图象H与x轴的交点为（﹣2，0），

∴图象M与x轴的交点为（﹣2，0）与（4，0），

∵图象M所对应的函数值小于0，

∴x＜﹣2或x＞4．