题目内容
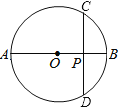
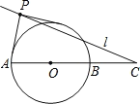
【题目】如图,已知⊙O 的半径长为2,点C为直径AB的延长线上一点,且BC=2.过点C任作一条直线l.若直线l上总存在点P,使得过点P所作的⊙O 的两条切线互相垂直,则∠ACP的最大值等于__________°.
【答案】45
【解析】
根据切线的性质和已知条件先证得四边形PMON是正方形,从而求得OP= ![]() ,以O为圆心,以
,以O为圆心,以![]() 长为半径作大圆⊙O,然后过C点作大⊙O的切线,切点即为P点,此时∠ACP有最大值,作出图形,根据切线的性质得出OP⊥PC,根据勾股定理求得PC的长,从而证得△OPC是等腰直角三角形,即可证得∠ACP的最大值为45°.
长为半径作大圆⊙O,然后过C点作大⊙O的切线,切点即为P点,此时∠ACP有最大值,作出图形,根据切线的性质得出OP⊥PC,根据勾股定理求得PC的长,从而证得△OPC是等腰直角三角形,即可证得∠ACP的最大值为45°.
∵PM、PN是过P所作的⊙O的两切线且互相垂直,
∴∠MON=90°,
∴四边形PMON是正方形,
根据勾股定理求得![]() ,
,
∴P点在以O为圆心,以![]() 长为半径作大圆⊙O上,
长为半径作大圆⊙O上,
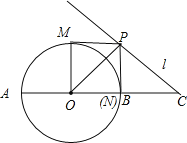
以O为圆心,以![]() 长为半径作大圆⊙O,然后过C点作大⊙O的切线,切点即为P点,此时∠ACP有最大值,如图所示,
长为半径作大圆⊙O,然后过C点作大⊙O的切线,切点即为P点,此时∠ACP有最大值,如图所示,
 ,
,
∵PC是大圆⊙O的切线,
∴OP⊥PC,∵OC=4,OP= ![]() ,
,
∴PC= ![]() ,
,
∴OP=PC,
∴∠ACP=45°,
∴∠ACP的最大值等于45°.故答案为45.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目