题目内容
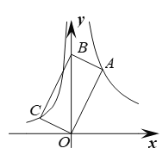
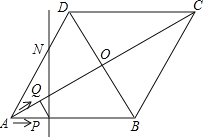
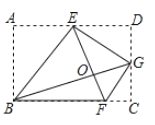
【题目】将矩形ABCD按如图所示的方式折叠，BE，EG，FG为折痕，若顶点A，C，D都落在点O处，且点B，O，G在同一条直线上，同时点E，O，F在另一条直线上，则
的值为（ ）
A.
B.
C.
D.
【答案】B
【解析】
由折叠可得，E，G分别为AD，CD的中点，设CD=2a，AD=2b，根据Rt△BCG中，CG2+BC2=BG2，可得即a2+（2b）2=（3a）2，进而得出
的值．
由折叠可得，AE=OE=DE，CG=OG=DG，
∴E，G分别为AD，CD的中点，
设CD=2a，AD=2b，则AB=2a=OB，DG=OG=CG=a，BG=3a，BC=AD=2b，
∵∠C=90°，
∴Rt△BCG中，CG2+BC2=BG2，
即a2+（2b）2=（3a）2，
∴b2=2a2，
即b=
a，
∴
＝，
∴的值为，
故选：B．
【题目】攀枝花得天独厚，气候宜人，农产品资源极为丰富，其中晚熟芒果远销北上广等大城市．某水果店购进一批优质晚熟芒果，进价为10元/千克，售价不低于15元/千克，且不超过40元/每千克，根据销售情况，发现该芒果在一天内的销售量
（千克）与该天的售价
（元/千克）之间的数量满足如下表所示的一次函数关系．
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
（1）某天这种芒果售价为28元/千克．求当天该芒果的销售量
（2）设某天销售这种芒果获利
元，写出与售价之间的函数关系式．如果水果店该天获利400元，那么这天芒果的售价为多少元？
【题目】某书店以
元的价格购进一批科普书进行销售，物价局根据市场行情规定，销售单价不低于
元且不高于
元．在销售中发现，该科普书的每天销售数量
（本）与销售单价
（元）之间存在某种函数关系，对应如下：
销售单价 |
|
|
|
|
|
销售数量 |
|
|
|
|
|
（1）用你所学过的函数知识，求出与之间的函数关系式；
（2）请问该科普书每天利润
（元）的最大值是多少？
（3）如果该科普书每天利润必须不少于
元，试求出每天销售数量最少为多少本？
【题目】某便利店的咖啡单价为10元/杯，为了吸引顾客，该店共推出了三种会员卡，如下表：
会员卡类型 | 办卡费用/元 | 有效期 | 优惠方式 |
A类 | 40 | 1年 | 每杯打九折 |
B类 | 80 | 1年 | 每杯打八折 |
C类 | 130 | 1年 | 一次性购买2杯，第二杯半价 |
例如，购买A类会员卡，1年内购买50次咖啡，每次购买2杯，则消费
元．若小玲1年内在该便利店购买咖啡的次数介于75~85次之间，且每次购买2杯，则最省钱的方式为（ ）
A.购买A类会员卡B.购买B类会员卡
C.购买C类会员卡D.不购买会员卡