题目内容
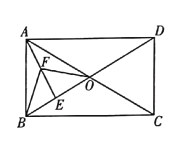
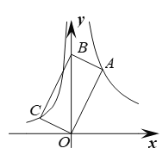
【题目】如图，四边形ABCO为矩形，点A在反比例函数y=
(x>0)的图象上，点C在反比例函数y=－
(x<0)的图象上，若点B在y轴上，则点A的坐标为_______．
【答案】
【解析】
连接AC交BO于E，过点C作CM⊥x轴，垂足为M，过点A作AN⊥x轴，垂足为N．先通过矩形的性质得到CE=AE，进一步得到MO=NO，设A(a，
)，则C点坐标为（-a，
）;然后在说明△CMO∽△ONA,最后根据相似三角形的性质列方程解答即可．
解：连接AC交BO于E，过点C作CM⊥x轴，垂足为M，过点A作AN⊥x轴，垂足为N．
∵四边形ABCO是矩形
∴CE=BE=AE=OE，∠AOC=90°
∵点E在y轴上
∴∠CMO=∠EON=∠ANO=90°
∴CM∥EO∥AN
∵CE=AE
∴MO=NO
∵点A在反比例函数y=
的图像上，
∴设A(a，)
∴MO=NO=a
又∵点C在反比例函数y=－
的图象上
∴C（-a，）
∴CM=
又∵∠COA=90°
∴∠AON + ∠COM=90°，
又∵∠MCO+ ∠COM=90，
∴∠AON=∠MCO，
又∵∠CMO=∠ANO=90°
∴△CMO∽△ONA，
∴
,
∴OM·ON=CM·AN，
∴a2=·=
∴a2 =2
∵a>0，
∴a=
，=
=2
故答案为．
【题目】二次函数
的图象与
轴交于
、
两点，点
，与
轴交于点
．
（1）
_________，
_________；
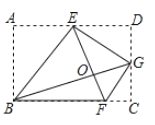
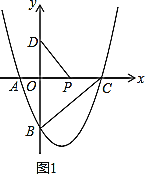
（2）如图1，
是轴上一动点，点
在轴上，连接
，求
的最小值；
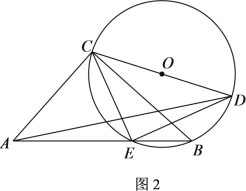
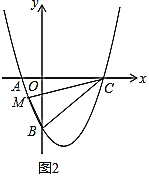
（3）如图2，点
在抛物线上，若
，求点的坐标．
【题目】甲、乙两个药店销售同一种口罩，在甲药店，不论一次购买数量是多少，价格均为3元/个；在乙药店，一次性购买数量不超过100个时，价格为3.5元/个；一次性购买数量超过100个时，其中100个的价格仍为3.5元/个，超过100个的部分的价格为2.5元/个．
（1）根据题意填表：
一次性购买数量(个) | 50 | 100 | 150 |
甲药店花费(元) |
| 300 |
|
乙药店花费(元) |
| 300 |
|
（2）当一次性购买多少个口罩时，在乙药店购买比在甲药店购买可以节约100元？
