Question

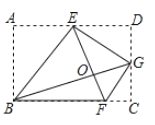
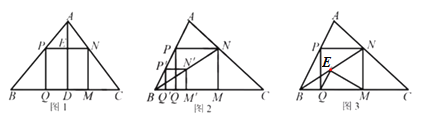
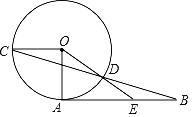
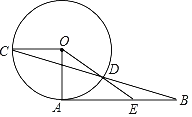
【题目】如图，AB是⊙O的切线，OA，OC是⊙O的半径，且OC∥AB，连接BC交⊙O于点D，点D恰为BC的中点，连接OD并延长，交AB于点E．

（1）求∠B的度数；

（2）求的值．

Answer 1

【答案】（1）15°；（2） ．

【解析】

（1）依据△COD≌△BED（AAS），即可得到OD=DE=OA=OC=BE，进而得到∠AEO=30°，再根据外角性质，即可得到∠B＝∠AEO＝15°．
（2）设OA=OC=a，则BE=a．依据∠AEO=30°，即可得到AE＝a，AB＝a+a＝(+1)a，进而得出的值．

解：（1）∵OC∥AB，

∴∠OCD＝∠EBD，∠COD＝∠BED．

又∵CD＝BD，

∴△COD≌△BED（AAS），

∴OC＝BE，OD＝DE，

∴OD＝DE＝OA＝OC＝BE，

∴∠B＝∠EDB．

∵AB是⊙O的切线，

∴OA⊥AB，

∴∠OAE＝90°，

∴sin∠AEO==.

∴∠AEO＝30°，

∴∠B＝∠AEO＝15°．

（2）设OA＝OC＝a，则BE＝a．

在Rt△AOE中，∠AEO＝30°，则AE＝a，

∴AB＝a+a＝(+1)a，

∴=+1.