题目内容
【题目】攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间的数量满足如下表所示的一次函数关系.
(元/千克)之间的数量满足如下表所示的一次函数关系.
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天这种芒果售价为28元/千克.求当天该芒果的销售量
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
【答案】(1)芒果售价为28元/千克时,当天该芒果的销售量为32千克;(2)这天芒果的售价为20元
【解析】
(1)用待定系数求出一次函数解析式,再代入自变量的值求得函数值;
(2)根据利润=销量×(售价成本),列出m与x的函数关系式,再由函数值求出自变量的值.
解:(1)设该一次函数解析式为![]()
则![]() ,解得:
,解得:![]()
∴![]() (
(![]() )
)
∴当![]() 时,
时,![]() ,
,
∴芒果售价为28元/千克时,当天该芒果的销售量为32千克
(2)由题易知![]()
![]()
![]() ,
,
当![]() 时,则
时,则![]()
整理得:![]()
解得:![]() ,
,![]()
∵![]()
∴![]()
所以这天芒果的售价为20元

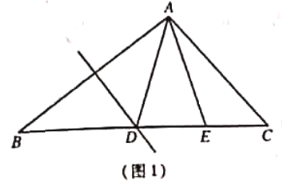
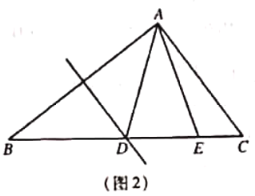
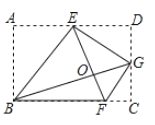
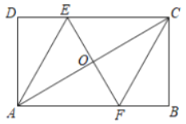
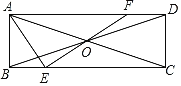
【题目】如图,在矩形ABCD中,AB=1,BC=3,AC和BD交于点O,点E是边BC上的动点(不与点B,C重合),连接EO并延长交AD于点F,连接AE,若△AEF是等腰三角形,则DF的长为_____.
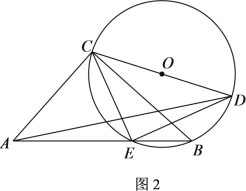
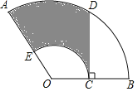
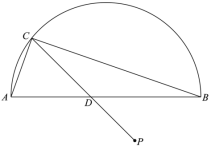
【题目】如图,![]() 是半圆的直径,P是半圆与直径
是半圆的直径,P是半圆与直径![]() 所围成的图形的外部的一定点,D是直径
所围成的图形的外部的一定点,D是直径![]() 上一动点,连接
上一动点,连接![]() 并延长,交半圆于点C,连接
并延长,交半圆于点C,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 两点之间的距离为
两点之间的距离为![]() 两点之间的距离为
两点之间的距离为![]() .
.
小明根据学习函数的经验,分别对函数![]() 随自变量x的变化而变化的规律进行了探究.
随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表自变量x的值进行取点、画图、测量,分别得到![]() 与x的几组对应值;
与x的几组对应值;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0.47 | 1.31 | 5.02 | 5.91 | 6 | |
| 6 | 5.98 | 5.86 | 5.26 | 3.29 | 1.06 | 0 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;
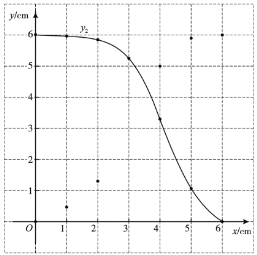
(3)结合函数图象,解决问题:当![]() 有一个角的正弦值为
有一个角的正弦值为![]() 时,
时,![]() 的长约为_____cm.
的长约为_____cm.