题目内容
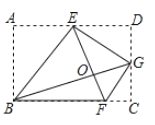
【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q先以2![]() cm/s的速度沿A→O的路线向点O运动,然后再以2cm/s的速度沿O→D的路线向点D运动,当P、Q到达终点时,整个运动随之结束,设运动时间为t秒.
cm/s的速度沿A→O的路线向点O运动,然后再以2cm/s的速度沿O→D的路线向点D运动,当P、Q到达终点时,整个运动随之结束,设运动时间为t秒.
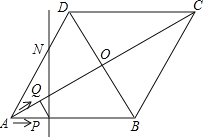
(1)在点P在AB上运动时,判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①直接写出当△PQM是直角三角形时t的取值范围;
②是否存在这样的t,使△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
【答案】(1)PQ⊥AC,理由见解析;(2)①0<t<5或t=7.5;②存在,t=2或![]()
【解析】
(1)利用相似三角形的性质解决问题即可.
(2)①分两种情形分别求解即可.
②假设存在这样的t,使得△PMN是以PN为一直角边的直角三角形,但是需分点N在AD上时和点N在CD上时两种情况分别讨论.
(1)由题意AP=4t,AQ=2![]() t.
t.
则![]() =
=![]() =
=![]() ,
,
又∵AO=10![]() ,AB=20,
,AB=20,
∴![]() =
=![]() =
=![]() .
.
∴![]() =
=![]() ,
,
又∵∠CAB=30°,
∴△APQ∽△ABO.
∴∠AQP=∠AOB=90°,即PQ⊥AC.
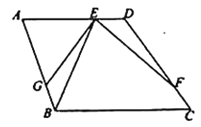
(2)①由(1)可知,当0<t<5时,如图1中,∠PQM=90°,△PQM是直角三角形,
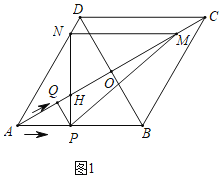
当5<t<10时,如图2中,当BP=PC时,∠PMQ=90°,此时t=7.5,
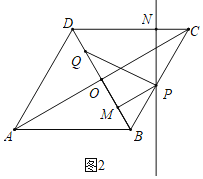
综上所述,当0<t<5或t=7.5时,△PQM是直角三角形
②存在这样的t,使△PMN是以PN为一直角边的直角三角形.
设l交AC于H.
如图1,当点N在AD上时,若PN⊥MN,则∠NMH=30°.
∴MH=2NH.得20![]() ﹣4
﹣4![]() t﹣
t﹣![]() t=2×
t=2×![]() ,解得t=2.
,解得t=2.
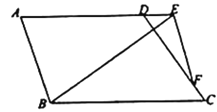
如图3,当点N在CD上时,若PM⊥PN,则PM∥CD,
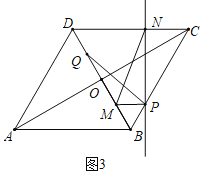
∴∠BPM=∠BCD=60°,∠BMP=∠BDC=60°,
∵∠PBM=60°,
∴△PBM是等边三角形,
∵PB=BM,
∴4t﹣20=![]() [20﹣2×2(t﹣5)],
[20﹣2×2(t﹣5)],
解得t=![]() .
.
故当t=2或![]() 时,存在以PN为一直角边的直角三角形.
时,存在以PN为一直角边的直角三角形.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案