题目内容
【题目】在平面直角坐标系中,如果点P(x,y)的坐标满足x+y=xy,那么称P为和谐点.
(1)若点A(a,2)是正比例函数y=kx(k≠0,k为常数)上的一个和谐点,求这个正比例函数的解析式;
(2)试判断函数y=﹣2x+1的图象上是否存在和谐点?若存在,求出和谐点的坐标;若不存在,请说明理由;
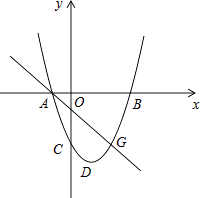
(3)直线l:y=kx+2经过和谐点P,且与反比例函数G:y=﹣ ![]() 交于M、N两点,若点P的纵坐标为3,求出直线l的解析式,并在x轴上找一点Q使得QM+QN最小.
交于M、N两点,若点P的纵坐标为3,求出直线l的解析式,并在x轴上找一点Q使得QM+QN最小.
【答案】
(1)
解:∵点A(a,2)是正比例函数y=kx(k≠0,k为常数)上的一个和谐点,
∴a+2=2a,
∴a=2,
∴A(2,2),
∴2=2k,
∴k=1,
∴正比例函数的解析式为y=x
(2)
解:不存在.理由如下,
设M(a,b)是函数y=﹣2x+1的图象上和谐点,
则有 ![]() ,消去b得,a﹣2a+1=a(﹣2a+1),整理得2a2﹣2a+1=0,
,消去b得,a﹣2a+1=a(﹣2a+1),整理得2a2﹣2a+1=0,
∵△=4﹣8=﹣4<0,
∴方程无解,
∴函数y=﹣2x+1的图象上不存在和谐点
(3)
解:由题意假设P(x,3),则x+3=3x,
∴x= ![]() ,
,
∴P( ![]() ,3),代入y=kx+2得3=
,3),代入y=kx+2得3= ![]() k+2,
k+2,
∴k= ![]() ,
,
∴直线l的解析式的解析式为y= ![]() x+2,
x+2,
由 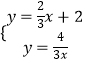 解得
解得 ![]() 或
或 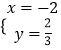 ,
,
不妨设M(﹣1, ![]() ),N(﹣2,
),N(﹣2, ![]() ),如图,作点N关于x轴的对称点N′,连接MN′交x轴于Q,此时NQ+QM最小.
),如图,作点N关于x轴的对称点N′,连接MN′交x轴于Q,此时NQ+QM最小.
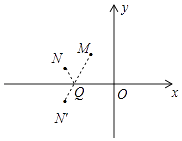
∵N′(﹣2,﹣ ![]() ),M(﹣1,
),M(﹣1, ![]() ),
),
∴直线MN′的解析式为y=2x+ ![]() ,
,
令y=0得到,x=﹣ ![]() ,
,
∴点Q的坐标为(﹣ ![]() ,0)
,0)
【解析】(1)根据和谐点,列出方程求出a以及点A坐标,即可解决问题.(2)不存在.设M(a,b)是函数y=﹣2x+1的图象上和谐点,则有 ![]() ,消去b得,a﹣2a+1=a(﹣2a+1),整理得2a2﹣2a+1=0,由△=4﹣8=﹣4<0,可知方程无解,由此即可判断.(3)首先根据和谐点的定义求出点P的坐标,即可求出直线l的解析式,利用方程组求出点M、N的坐标,如图,作点N关于x轴的对称点N′,连接MN′交x轴于Q,此时NQ+QM最小.求出直线N′M的解析式即可解决问题.
,消去b得,a﹣2a+1=a(﹣2a+1),整理得2a2﹣2a+1=0,由△=4﹣8=﹣4<0,可知方程无解,由此即可判断.(3)首先根据和谐点的定义求出点P的坐标,即可求出直线l的解析式,利用方程组求出点M、N的坐标,如图,作点N关于x轴的对称点N′,连接MN′交x轴于Q,此时NQ+QM最小.求出直线N′M的解析式即可解决问题.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案