Question

【题目】已知在平面直角坐标系xOy中，O为坐标原点，二次函数y=x2+bx的图象经过点A（﹣1，4），交x轴于点B（a，0）．
（1）求a与b的值；
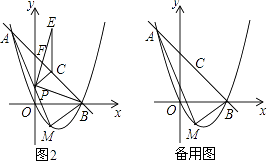
（2）如图1，点M为抛物线上的一个动点，且在直线AB下方，试求出△ABM面积的最大值及此时点M的坐标；

（3）在（2）的条件下，点C为AB的中点，点P是线段AM上的动点，如图2所示，问AP为何值时，将△BPC沿边PC翻折后得到△EPC，使△EPC与△APC重叠部分的面积是△ABP的面积的 ．

Answer 1

【答案】
（1）

解：把A（﹣1，4）代入y=x2+bx得到4=1﹣b，

∴b=﹣3，

∴y=x2﹣3x，

∵B（a，0）在函数图象上，

∴a2﹣3a=0，

∴a=3或0（舍弃），

∴a=3

（2）

解：如图1中，作MG∥y轴交AB于G．

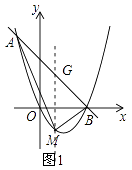
设直线AB解析式为y=kx+b，把（﹣1，4），（3，0）代入得 ，解得 ，

∴y=﹣x+3，设M（x，x2﹣3x），则G（m，﹣m+3），

∴S△ABM=S△AMG+S△BMG= ×4×[（﹣x+3）﹣（x2﹣3x）=﹣2x2+4x+6=﹣2（x﹣1）2+8，

∵﹣2＜0，

∴当x=1时，△ABM的面积最大，最大值为8，

此时M（1，﹣2）．

（3）

解：如图2中，连接AF．

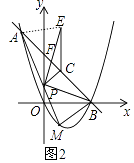
∵C为AB中点，△EPC与△APC重叠部分的面积是△ABP的面积的 ，

∴F为AC与EP的中点，连接AE，

∴四边形APCE是平行四边形，

∴AP=EC=BC= AB=2

【解析】（1）把A（﹣1，4）代入y=x2+bx求出b，再把B（a，0）代入抛物线的解析式即可解决问题．（2）如图1中，作MG∥y轴交AB于G．设M（x，x2﹣3x），则G（m，﹣m+3），根据S△ABM=S△AMG+S△BMG构建二次函数，利用二次函数的性质解决问题．（3）如图2中，连接AF．只要证明四边形APCE是平行四边形，即可解决问题．