题目内容
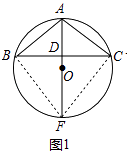
【题目】如图，△ABC内接于⊙O，直径AF平分∠BAC，交BC于点D． 
（1）如图1，求证：AB=AC；
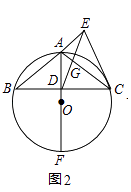
（2）如图2，延长BA到点E，连接ED、EC，ED交AC于点G，且ED=EC，求证：∠EGC=∠ECA+2∠ACB；
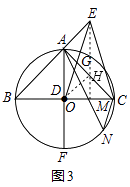
（3）如图3，在（2）的条件下，当BC是⊙O的直径时，取DC的中点M，连接AM并延长交圆于点N，且EG=5，连接CN并求CN的长．
【答案】
（1）证明：如图1，连接BF、CF，
∵AF是⊙O的直径，
∴∠ABF=∠ACF=90°，
∵AF平分∠BAC，
∴∠BAF=∠CAF，
∴∠AFB=∠AFC，
∴ 
，
∴AB=AC
（2）证明：如图2，∵ED=EC，
∴∠EDC=∠ECD，
∵∠EGC=∠ACB+∠EDC，
∴∠EGC=∠ACB+∠ECD=∠ACB+∠ACB+∠ECA=∠ECA+2∠ACB
（3）证明：如图3，连接EM，交AC于H，连接OH，
∵ED=EC，M是DC的中点，
∴EM⊥DC，
∴∠BME=90°，
∵BC为⊙O 的直径，
∴∠BAC=90°，
∵AB=AC，
∴∠B=45°，
∴△BME是等腰直角三角形，
∴∠BEM=45°，
∴△EAH是等腰直角三角形，
∴AE=AH，
∵AB=AC，OB=OC，
∴AO⊥BC，AO=OB=OC= 
BC，
∵∠AOC=∠HMC=90°，
∴MH∥AO，
∵M是OC的中点，
∴H是AC的中点，
∴AH=CH=OH，OH⊥AC，
∴AE=OH，
∵∠EAH=∠AHO=90°，
∴AE∥OH，
∴四边形AOHE是平行四边形，
∴AG=GH，EG=OG=5，
设AG=x，则GH=x，OH=2x，
在Rt△OGH中，52=x2+（2x）2，
x= 
，
∴AG=GH= 
，OH=HC=2 ，AC=4 ，
∴AO= 
= 
=2 
，
∴OC=2 ，
∴MC= OC= ，
在Rt△AOM中，AM= 
= 
=5 
，
∵∠N=∠B=45°，
∴∠N=∠ACB=45°，
∵∠NAC=∠MAC，
∴△AMC∽△ACN，
∴ 
，
∴ 
，
∴CN=4．
【解析】（1）连接BF、CF，根据角平分线和直径所对的圆周角是直角得：∠AFB=∠AFC，则所对的弧相等，弦相等；（2）根据等腰三角形的性质：等边对等角得：∠EDC=∠ECD，再由外角定理得：∠EGC=∠ACB+∠EDC，等量代换可得结论；（3）作辅助线，构建高线和中位线，①证明四边形AOHE是平行四边形，得AG=GH，EG=OG=5，②设AG=x，则GH=x，OH=2x，分别计算AG，OH，AC，AO，AM的长；③证明△AMC∽△ACN，列比例式可求得CN的长．
