Question

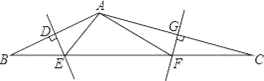
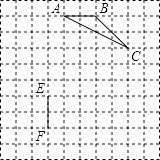
【题目】已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=50°

（1）求证：①AC=BD；②∠APB=50°；

（2）如图②，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系为 ，∠APB的大小为

Answer 1

【答案】（1）见解析；（2）AC=BD，α．

【解析】

试题分析：（1）根据∠AOB=∠COD=50°求出∠AOC=∠BOD，根据SAS推出△AOC≌△BOD，根据全等三角形的性质得出AC=BD，∠CAO=∠DBO，

根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB，推出∠APB=∠AOB即可．

（2）根据∠AOB=∠COD=50°求出∠AOC=∠BOD，根据SAS推出△AOC≌△BOD，根据全等三角形的性质得出AC=BD，∠CAO=∠DBO，

根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB，推出∠APB=∠AOB即可．

证明：（1）∵∠AOB=∠COD=50°，

∴∠AOC=∠BOD，

在△AOC和△BOD中，

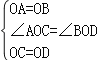
∴△AOC≌△BOD，

∴AC=BD，∠CAO=∠DBO，

根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB，

∴∠APB=∠AOB=50°．

（2）解：AC=BD，∠APB=α，

理由是：）∵∠AOB=∠COD=50°，

∴∠AOC=∠BOD，

在△AOC和△BOD中，

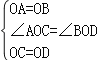
∴△AOC≌△BOD，

∴AC=BD，∠CAO=∠DBO，

根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB，

∴∠APB=∠AOB=α，

故答案为：AC=BD，α．