题目内容
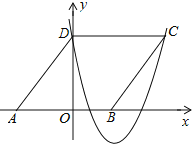
【题目】某种蔬菜的单价![]() 与销售月份x之间的关系如图1所示,成本
与销售月份x之间的关系如图1所示,成本![]() 与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
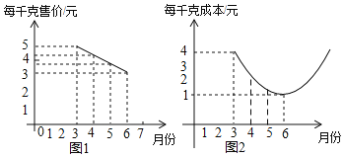
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的利润是 元.(利润=售价-成本);
(2)设每千克该蔬菜销售利润为P,请列出x与P之间的函数关系式,并求出哪个月出售这种蔬菜每千克的利润最大,最大利润是多少?
【答案】(1)2;(2)5月时利润最大,最大利润为![]() 元.
元.
【解析】
(1)找出当x=6时,y1、y2的值,二者做差即可得出结论;
(2)观察图象找出点的坐标,利用待定系数法即可求出y1、y2关于x的函数关系式,二者做差后利用二次函数的性质即可解决最值问题.
(1)当x=6时,y1=3,y2=1.
∵y1﹣y2=3﹣1=2,∴6月份出售这种蔬菜每千克的收益是2元.
(2)设y1=mx+n,y2=a(x﹣6)2+1.
将(3,5)、(6,3)代入y1=mx+n,得![]() ,解得:
,解得: ,∴y1
,∴y1![]() x+7;
x+7;
将(3,4)代入y2=a(x﹣6)2+1,4=a(3﹣6)2+1,解得:a![]() ,∴y2
,∴y2![]() (x﹣6)2+1
(x﹣6)2+1![]() x2﹣4x+13,∴P=y1﹣y2
x2﹣4x+13,∴P=y1﹣y2![]() x+7﹣(
x+7﹣(![]() x2﹣4x+13)
x2﹣4x+13)![]() x2
x2![]() x﹣6
x﹣6![]() (x﹣5)2
(x﹣5)2![]() .
.
∵![]() 0,∴当x=5时,P取最大值,最大值为
0,∴当x=5时,P取最大值,最大值为![]() .
.
答:5月份出售这种蔬菜,每千克的收益最大,最大利润是![]() 元/千克.
元/千克.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目