题目内容
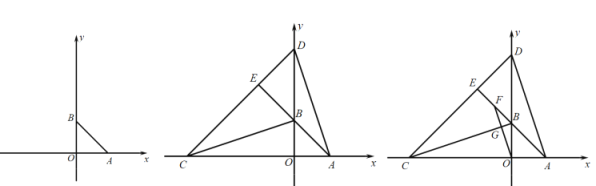
【题目】)如图,Rt△ABC中,C= 90o,以斜边AB为边向外作正方形 ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6![]() ,则另一直角边BC的长为 ▲ .
,则另一直角边BC的长为 ▲ .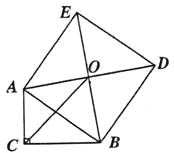
【答案】7。
【解析】
正方形的性质,全等三角形的判定和性质,矩形的判定和性质,等腰直角三角形的判定和性质,勾股定理。
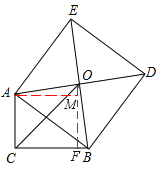
∵四边形ABDE为正方形,∴∠AOB=90°,OA=OB。
∴∠AOM+∠BOF=90°。
又∵∠AMO=90°,∴∠AOM+∠OAM=90°。∴∠BOF=∠OAM。
在△AOM和△BOF中,
∵∠AMO=∠OFB=90°,∠OAM=∠BOF, OA=OB,
∴△AOM≌△BOF(AAS)。∴AM=OF,OM=FB。
又∵∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形。∴AM=CF,AC=MF=5。
∴OF=CF。∴△OCF为等腰直角三角形。
∵OC=6![]() ,∴根据勾股定理得:CF2+OF2=OC2,即2CF2=(6
,∴根据勾股定理得:CF2+OF2=OC2,即2CF2=(6![]() )2,解得:CF=OF=6。
)2,解得:CF=OF=6。
∴FB=OM=OF-FM=6-5=1。∴BC=CF+BF=6+1=7。

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目