题目内容
【题目】如图,点A(a,1)、B(﹣1,b)都在函数![]() (x<0)的图象上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是 .
(x<0)的图象上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是 .

【答案】y=x+2
【解析】
试题分析:作点A关于x轴的对称点A′,作点B关于y轴的对称点B′,连接A′B′,分别于x、y轴交于点P、Q点,此时四边形PABQ的周长最小,由点A、B均为反比例函数上的点,由此即可求出a、b值,即得出点A、B的坐标,再根据对称的性质找出点A′、B′的坐标,结合两点的坐标利用待定系数法即可求出PQ所在直线的解析式.
解:作点A关于x轴的对称点A′,作点B关于y轴的对称点B′,连接A′B′,分别于x、y轴交于点P、Q点,此时四边形PABQ的周长最小,如图所示.
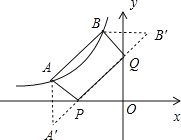
∵点A(a,1)、B(﹣1,b)都在函数![]() (x<0)的图象上,
(x<0)的图象上,
∴a=﹣3÷1=﹣3,b=﹣3÷(﹣1)=3,
∴点A(﹣3,1),点B(﹣1,3),
∴点A′(﹣3,﹣1),点B′(1,3).
设直线A′B′的解析式为y=kx+c,
∴![]() ,解得:
,解得:![]() ,
,
∴直线A′B′的解析式为y=x+2,即PQ所在直线的解析式是y=x+2.
故答案为:y=x+2.

练习册系列答案
相关题目