题目内容
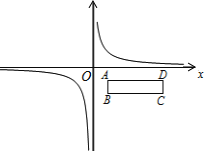
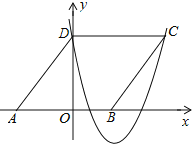
【题目】如图，在平面直角坐标系中，菱形ABCD的顶点A在x轴负半轴上，顶点B在x轴正半轴上．若抛物线p=ax2-10ax+8（a＞0）经过点C、D，则点B的坐标为________．
【答案】（4，0）
【解析】
根据抛物线p＝ax210ax＋8（a＞0）经过点C、D和二次函数图象具有对称性，可以求得该抛物线顶点的横坐标和CD的长，然后根据菱形的性质和勾股定理可以求得AO的长，从而可以求得OB的长，进而写出点B的坐标．
解：∵抛物线p＝ax210ax＋8＝a（x5）225a＋8，
∴该抛物线的顶点的横坐标是x＝5，当x＝0时，y＝8，
∴点D的坐标为：（0，8），
∴OD＝8，
∵抛物线p＝ax210ax＋8（a＞0）经过点C、D，CD∥AB∥x轴，
∴CD＝5×2＝10，
∴AD＝10，
∵∠AOD＝90°，OD＝8，AD＝10，
∴AO＝
，
∵AB＝10，
∴OB＝10AO＝106＝4，
∴点B的坐标为（4，0），
故答案为：（4，0）
【题目】在“朗读者”节目的影响下，某中学在暑期开展了“好书伴我成长”读书话动，并要求读书要细读，最少要读完2本书，最多不建议超过5本。初一年级5个班，共200名学生，李老师为了了解学生暑期在家的读书情况，给全班同学布置了一项调查作业：了解初一年级学生暑期读书情况.班中三位同学各自对初一年级读书情况进行了抽样调查，并将数据进行了整理，绘制的统计图表分别为表1、表2、表3.
表1：在初一年级随机选择5名学生暑期读书情况的统计表
阅读书数量（本） | 2 | 3 | 4 | 5 |
人数 | 2 | 1 | 1 | 1 |
表2：在初一年级“诵读班”班随机选取20名学生暑期读书情况的统计表
阅读书数量（本） | 2 | 3 | 4 | 5 |
人数 | 0 | 1 | 4 | 15 |
表3：在初一年级随机选取20名学生暑期读书情况的统计表
阅读书数量（本） | 2 | 3 | 4 | 5 |
人数 | 2 | 8 | 6 | 4 |
问题1：根据以上材料回答：三名同学中，哪一位同学的样本选取更合理，并简要说明其他两位同学选取样本的不足之处；
老师又对合理样本中的所有学生进行了“阅读动机”的调研，并制作成了如下统计图.
问题2：通过统计图的信息你认为“阅读动机”
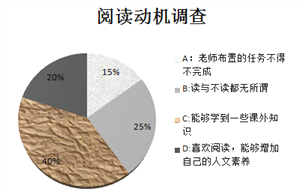
在“40%”的群体，暑期读几本书的可能性大，并说出你的理由.
【题目】食品厂从生产的袋装食品中抽出样品
袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负来表示，记录如下表；
与标准质量的差值（单位：克） |
|
|
|
|
|
|
袋数 |
|
|
|
|
|
|
（1）这批样品的平均质量比标准质量是超过还是不足？平均每袋超过或不足多少克？
（2）若每袋标准质量为
克，求抽样检测的样品总质量是多少？
