题目内容
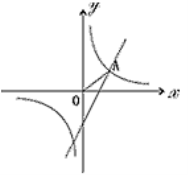
【题目】如图,已知反比例函数![]() 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
(1)求反比例函数的解析式;
(2)如图,已知点A在第一象限,且同时在上述两个函数的图象上, 求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由。
【答案】(1)y=![]() ;(2)(1,1);(3)符合条件的点有4个,分别是(
;(2)(1,1);(3)符合条件的点有4个,分别是(![]() ,0),(-
,0),(-![]() ,0),(2,0),(1,0).
,0),(2,0),(1,0).
【解析】
试题分析:(1)把过一次函数的两个点代入一次函数,即可求得k,进而求得反比例函数的解析式;(2)同时在这两个函数解析式上,让这两个函数组成方程组求解即可;(3)应先求出OA的距离,然后根据:OA=OP,OA=AP,OP=AP,分情况讨论解决.
试题解析:(1)由题意得 ![]() ,②-①得:k=2,∴反比例函数的解析式为y=
,②-①得:k=2,∴反比例函数的解析式为y=![]() ;
;
(2)由 ,解得
,解得![]() ,
,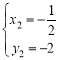 ,∵点A在第一象限,∴点A的坐标为(1,1);
,∵点A在第一象限,∴点A的坐标为(1,1);
(3)OA=![]() =
=![]() ,OA与x轴所夹锐角为45°,①当OA为腰时,由OA=
,OA与x轴所夹锐角为45°,①当OA为腰时,由OA=![]() 得
得![]() (
(![]() ,0),由OA=
,0),由OA=![]() 得
得![]() (-
(-![]() ,0);由OA=
,0);由OA=![]() 得
得![]() (2,0).②当OA为底时,
(2,0).②当OA为底时,![]() =
=![]() 得
得![]() (1,0).
(1,0).
∴符合条件的点有4个,分别是(![]() ,0),(-
,0),(-![]() ,0),(2,0),(1,0).
,0),(2,0),(1,0).


【题目】某校一间阶梯教室中,第1排的座位数为a,从第2排开始,每一排都比前一排增加两个座位.
(1)请你在下表的空格里填写一个适当的式子:
第1排的 座位数 | 第2排的 座位数 | 第3排的 座位数 | 第4排的 座位数 | … |
a | a+2 | a+4 | … |
(2)写出第n排座位数的表达式;
(3)求当a=20时,第10排的座位数是多少?若这间阶梯教室共有15排,那么最多可容纳多少学员?
【题目】某电信检修小组从A地出发,在东西向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下。(单位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
-3 | +7 | -9 | +8 | +6 | -5 | -4 |
(1)求收工时距A地多远?
(2)在第几次纪录时距A地最远?
(3)若每km耗油0.2升,问共耗油多少升?