Question

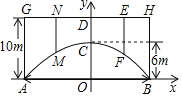
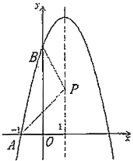
【题目】已知抛物线在坐标系中的位置如图所示，它与，轴的交点分别为，，是其对称轴上的动点，根据图中提供的信息，给出以下结论：①，②是的一个根，③若，，则.其中正确的有______个.

Answer 1

【答案】3

【解析】

①根据对称轴方程即可得结论；②根据对称轴和抛物线与x轴的一个交点坐标即可求出另一个交点坐标即可得结论；③构造PA和PB所在直角三角形全等，得线段相等，从而求得B点的坐标，再根据交点式求抛物线解析式，求当x＝1时，y的值即可得结论．

解：①因为抛物线的对称轴x＝1，
所以＝1，即b＋2a＝0，
所以①正确；
②因为A（1，0），对称轴x＝1，
所以设抛物线与x轴的另一个交点为E，
所以E（3，0），
所以x＝3时，y＝0，即x＝3是ax2＋bx＋c＝0的一个根．
所以②正确；
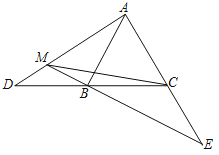
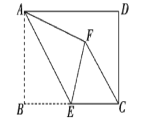
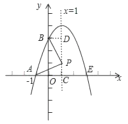
③如图：过点B作BD⊥对称轴于点D，设对称轴交x轴于点C，
∵AP⊥BP，
∴∠APB＝90°，
∴∠APC＋∠BPD＝90°，
∵∠BPD＋∠PBD＝90°，
∴∠PBD＝∠APC，
∵AP＝BP，
∴Rt△APC≌Rt△PBD（AAS）
∴PC＝BD＝1，DP＝AC＝2，
∴DC＝3，
∴OB＝3，
∴B（0，3）．又E（3，0），A（1，0）．
设抛物线解析式为y＝a（x＋1）（x3），
把B（0，3）代入，解得a＝1，
∴抛物线解析式为x2＋2x＋3，
当x＝1时，y＝4，
即a＋b＋c＝4．
所以③正确．
故答案为3．