��Ŀ����
����Ŀ��ij��˾��A�Ͳ�Ʒ40����B�Ͳ�Ʒ60��������������ס��������̵����ۣ�����70�����꣬30�����ҵ꣬�Ҷ������꣮���̵����������ֲ�Ʒÿ��������Ԫ�����±���
A������Ԫ/���� | B������Ԫ/���� | |
�� | 180 | 150 |
�ҵ� | 120 | 110 |
��1����������A�Ͳ�Ʒx������ҹ�˾������100����Ʒ��������ΪW��Ԫ������W����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2����Ҫ��������14960Ԫ���ж����ֲ�ͬ���䷽�������г����巽����
��3��Ϊ�˴�������˾�������Լ�A�Ͳ�Ʒ�������ۣ�ÿ������aԪ����������A�Ͳ�Ʒ��ÿ�������Ը��ڼ�B�Ͳ�Ʒ��ÿ�������B�Ͳ�Ʒ�Լ��ҵ��A��B�Ͳ�Ʒ��ÿ�����䣬�ù�˾�����Ʒ��䷽����ʹ������ﵽ���
���𰸡���1��W��20x+14200�� 10��x��40����2�������ֲ�ͬ�ķ��䷽����:��x��39ʱ����A��39����B��31�����ҵ�A��1����B��29������x��40ʱ����A��40����B��30�����ҵ�A��0����B��30������3���������.
��������
(1)��������ã���B�Ͳ�Ʒ�У�70��x�������ҵ�A���У�40��x������B���У�x��10����������ô���������ÿ����Ӧ��Ʒ���������Ӧ����֮�ͣ����ݸ����������Ʒ������Ϊ�Ǹ����ɵ��Ա�����ȡֵ��Χ��
(2)��(1)�еĴ���ʽ����14960�����(1)���Ա�����ȡֵ�ɵ���Ӧ�ķ��䷽����
(3)����������A�Ͳ�Ʒ��ÿ�������Ը��ڼ�B�Ͳ�Ʒ��ÿ������ɵ�a��ȡֵ�����(1)�õ���Ӧ����������a�IJ�ͬȡֵ�õ�����ĺ���Ӧ�õ������ֵ�ķ������ɣ�
�⣺��1��������ã���B�Ͳ�Ʒ�У�70��x�������ҵ�A���У�40��x������B���У�x��10������
��W��180x+150��70��x��+120��40��x��+110��x��10����20x+14200��
�� ��
��
���10��x��40��
��2����W��20x+14200��14960��
���x��38��
��38��x��40��x��39��40��
�������ֲ�ͬ�ķ��䷽����
��x��39ʱ����A��39����B��31�����ҵ�A��1����B��29����
��x��40ʱ����A��40����B��30�����ҵ�A��0����B��30����
��3�������⣺W����180��a��x+150��70��x��+120��40��x��+110��x��10������20��a��x+14200��
����0��a��20ʱ��20��a��0��W��x���������
��x��40��W�����ֵ��
����A��40����B��30�����ҵ�A��0����B��30������ʹ������ﵽ���
����a��20ʱ��10��x��40��W��16800����������ĸ��ַ�����ʹ������һ����
����20��a��30ʱ��20��a��0��W��x�������С��
��x��10��W�����ֵ��
����A��10����B��60�����ҵ�A��30����B��0������ʹ������ﵽ���

 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д�����Ŀ�������������̨���ʶ��ߡ���Ŀ�IJ��������ʶ���ΪԽ��Խ���ͬѧ��ϲ����������ij��ѧ�ƻ���ȫУ��չ���ʶ������Ϊ���˽�ͬѧ�Ƕ������IJ���̬�ȣ�����Բ���ѧ��������һ�ε��飬�������������ⲿ��ͬѧ��̬�Ȼ���Ϊ�ĸ����![]() .�������룬
.�������룬![]() .һ�����룬
.һ�����룬![]() .���Բ��룬
.���Բ��룬![]() .������.���ݵ��������������²�������ͳ�Ʊ���ͳ��ͼ.
.������.���ݵ��������������²�������ͳ�Ʊ���ͳ��ͼ.
ѧ�����롰�ʶ�����̬��ͳ�Ʊ�
��� | ���� | ��ռ�ٷֱ� |
| 18 |
|
| 20 |
|
|
|
|
| 4 |
|
�ϼ� |
|
|
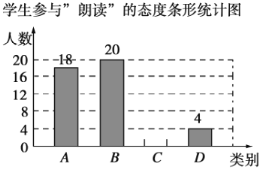
�������������Ϣ������������⣺
��1��![]() ______��
______��![]() ______����������ͳ��ͼ����������
______����������ͳ��ͼ����������
��2����У��1500��ѧ��������������롱������������150��ʱ�����ʶ��������˳����չ��ͨ�����������λ�ܷ�˳����չ��
��3�����ʶ�����У����꼶һ��Ƚ����������ͬѧǡ����������Ů���������ѡȡ�����ڰ༶�����ʶ�ʾ�������û���״ͼ�����б�������ѡ���˶���Ů���ĸ��ʣ����г����еȿ��ܵĽ��.