题目内容
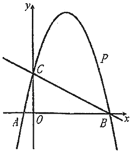
【题目】某坦克部队需要经过一个拱桥(如图所示),拱桥的轮廓是抛物线形,拱高OC=6m,跨度AB=20m,有5根支柱:AG、MN、CD、EF、BH,相邻两支柱的距离均为5m.
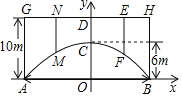
(1)以AB的中点为原点,AB所在直线为x轴,支柱CD所在直线为y轴,建立平面直角坐标系,求抛物线的解析式;
(2)若支柱每米造价为2万元,求5根支柱的总造价;
(3)拱桥下面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道是坦克的行进方向,现每辆坦克长4m,宽2m,高3m,行驶速度为24km/h,坦克允许并排行驶,坦克前后左右距离忽略不计,试问120辆该型号坦克从刚开始进入到全部通过这座长1000m的拱桥隧道所需最短时间为多少分钟?
【答案】(1)y=﹣![]() x2+6;(2)70万元;(3)2.9分
x2+6;(2)70万元;(3)2.9分
【解析】
(1)根据题目可知A,B,C的坐标,设出抛物线的解析式代入可求解.
(2)把x=5代入可求出支柱的长度,然后算出总造价即可.
(3)先求出坦克方队的长,然后算出速度,从而求得通过隧道的时间即可.
(1)设y=ax2+c,把C(0,6)、B(10,0)代入,
得![]() .
.
∴y=﹣![]() x2+6.
x2+6.
(2)当x=5时,y=﹣![]() ×52+6=
×52+6=![]() ,
,
∴EF=10﹣![]() =
=![]() ,CD=10﹣6=4,
,CD=10﹣6=4,
支柱的总造价为2(2×![]() +2×10+4)=70(万元).
+2×10+4)=70(万元).
(3)∵坦克的高为3米,令y=3时,﹣![]() x2+6=3,
x2+6=3,
解得:x=±5![]() ,
,
∵7<5![]() <8,坦克宽为2米,
<8,坦克宽为2米,
∴可以并排3辆坦克行驶,此时坦克方阵的长为120÷3×4=160(米),
坦克的行驶速度为24km/h=400米/分,
∴通过隧道的最短时间为![]() =2.9(分).
=2.9(分).

 名校课堂系列答案
名校课堂系列答案【题目】随着中央电视台《朗读者》节目的播出,“朗读”为越来越多的同学所喜爱,西宁市某中学计划在全校开展“朗读”活动,为了了解同学们对这项活动的参与态度,随机对部分学生进行了一次调查,调查结果整理后,将这部分同学的态度划分为四个类别:![]() .积极参与,
.积极参与,![]() .一定参与,
.一定参与,![]() .可以参与,
.可以参与,![]() .不参与.根据调查结果制作了如下不完整的统计表和统计图.
.不参与.根据调查结果制作了如下不完整的统计表和统计图.
学生参与“朗读”的态度统计表
类别 | 人数 | 所占百分比 |
| 18 |
|
| 20 |
|
|
|
|
| 4 |
|
合计 |
|
|
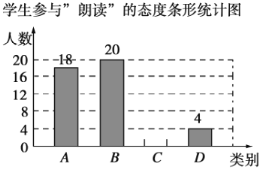
请你根据以上信息,解答下列问题:
(1)![]() ______,
______,![]() ______,并将条形统计图补充完整;
______,并将条形统计图补充完整;
(2)该校有1500名学生,如果“不参与”的人数不超过150人时,“朗读”活动可以顺利开展,通过计算分析这次活动能否顺利开展?
(3)“朗读”活动中,九年级一班比较优秀的四名同学恰好是两男两女,从中随机选取两人在班级进行朗读示范,试用画树状图法或列表法求所选两人都是女生的概率,并列出所有等可能的结果.