题目内容
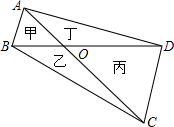
如图，不等长的两对角线AC、BD相交于O点，且将四边形ABCD分成甲、乙、丙、丁四个三角形．若OA：OC=OB：OD=1：2，则此四个三角形的关系，下列叙述何者正确（ ）
| A．甲丙相似，乙丁相似 |
| B．甲丙相似，乙丁不相似 |
| C．甲丙不相似，乙丁相似 |
| D．甲丙不相似，乙丁不相似 |
在△OAB和△OCD中，OA：OC=OB：OD，又∠AOB=∠COD
∴△OAB∽△OCD
即甲丙相似；
无法证明△OAD相似△OCB，乙丁不相似．
故选B．
∴△OAB∽△OCD
即甲丙相似；
无法证明△OAD相似△OCB，乙丁不相似．
故选B．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
