题目内容
【题目】已知在△ABC中,AB=AC=8,∠BAC=30°,将△ABC绕点A旋转,使点B落在原△ABC的点C处,此时点C落在点D处,延长线段AD,交原△ABC的边BC的延长线于点E,那么线段DE的长等于 .
【答案】![]()
【解析】解:过点C作CH⊥AE于H,如图,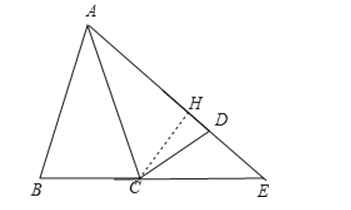
∵AB=AC=8,
∴∠B=∠ACB=![]() (180°﹣∠BAC)=
(180°﹣∠BAC)=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵△ABC绕点A旋转,使点B落在原△ABC的点C处,此时点C落在点D处,
∴AD=AB=8,∠CAD=∠BAC=30°,
∵∠ACB=∠CAD+∠E,
∴∠E=75°﹣30°=45°,
在Rt△ACH中,∵∠CAH=30°,
∴CH=![]() AC=4,AH=
AC=4,AH=![]() CH=4
CH=4![]() ,
,
∴DH=AD﹣AH=8﹣4![]() ,
,
在Rt△CEH中,∵∠E=45°,
∴EH=CH=4,
∴DE=EH﹣DH=4﹣(8﹣4![]() )=4
)=4![]() ﹣4.
﹣4.
故答案为4![]() ﹣4.
﹣4.
作CH⊥AE于H,根据等腰三角形的性质和三角形内角和定理可计算出∠ACB=![]() (180°﹣∠BAC)=75°,再根据旋转的性质得AD=AB=8,∠CAD=∠BAC=30°,则利用三角形外角性质可计算出∠E=45°,接着在Rt△ACH中利用含30度的直角三角形三边的关系得CH=
(180°﹣∠BAC)=75°,再根据旋转的性质得AD=AB=8,∠CAD=∠BAC=30°,则利用三角形外角性质可计算出∠E=45°,接着在Rt△ACH中利用含30度的直角三角形三边的关系得CH=![]() AC=4,AH=
AC=4,AH=![]() CH=4
CH=4![]() ,所以DH=AD﹣AH=8﹣4
,所以DH=AD﹣AH=8﹣4![]() ,然后在Rt△CEH中利用∠E=45°得到EH=CH=4,于是可得DE=EH﹣DH=
,然后在Rt△CEH中利用∠E=45°得到EH=CH=4,于是可得DE=EH﹣DH=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目