Question

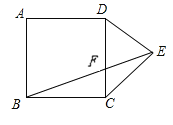
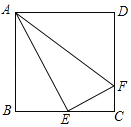
【题目】如图所示，在正方形ABCD中，E是BC的中点，F是CD上一点，AE⊥EF，下列结论：①∠BAE＝30°；②△ABE∽△AEF；③CD＝3CF；④S△ABE＝4S△ECF．其中正确的有_____（填序号）．

Answer 1

【答案】②④．

【解析】

由正方形的性质和三角函数得出∠BAE＜30°，①不正确；由题中条件可得△CEF∽△BAE，进而得出对应线段成比例，得出②正确，CF=13FD，③不正确；进而又可得出△ABE∽△AEF，得出④正确，即可得出题中结论．

解：tan∠BAE＝，

∴∠BAE≠30°，故①错误；

∵四边形ABCD是正方形，

∴∠B＝∠C＝90°，AB＝BC＝CD，

∵AE⊥EF，

∴∠AEF＝∠B＝90°，

∴∠BAE+∠AEB＝90°，∠AEB+FEC＝90°，

∴∠BAE＝∠CEF，

∴△BAE∽△CEF，

∴，

∵BE＝CE＝BC，

∴＝＝4，

∴S△ABE＝4S△ECF，故④正确；

∴CF＝EC＝CD，

∴CD＝4CF，

故③错误；

设CF＝a，则BE＝CE＝2a，AB＝CD＝AD＝4a，DF＝3a，

∴AE＝2a，EF＝a，AF＝5a，

∴，，

∴，

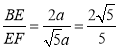∴△ABE∽△AEF，故②正确．

∴②与④正确．

故答案为：②④．