Question

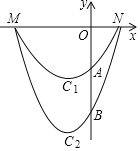
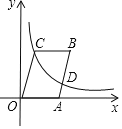
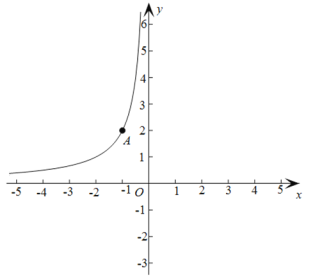
【题目】已知：在平面直角坐标系xOy中，点A（-1，2）在函数(x<0)的图象上．

（1）求m的值；

（2）过点A作y轴的平行线，直线与直线交于点B，与函数(x<0)的图象交于点C，与轴交于点D．

①当点C是线段BD的中点时，求b的值；

②当BC<BD时，直接写出b的取值范围．

Answer 1

【答案】（1）m= -2；（2）①b=3；②b> -3．

【解析】

（1）把A（-1，2）代入解析式即可求解；

（2）①根据题意知点B的横坐标为-1，点D的横坐标为0，由于点C是BD的中点，利用中点坐标公式即可求得点C的横坐标，代入中可求得点C的坐标，代入函数 中，即可求解；

②先利用①的方法求得BC=BD即点B是CD的中点时的值，观察图象，即可求得b的取值范围．

（1）把A（-1，2）代入函数(x<0)中，

∴ ；

（2）① 如图，

根据题意知：点B的横坐标为-1，点D的横坐标为0，

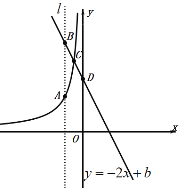
∵点C是BD的中点，

∴点C的横坐标为，

把代入函数中，得y = 4，

∴点C的坐标为（，4），

把点C的坐标为（，4）代入函数 中，

得：，

解得：；

② 当点B是CD的中点时，BC=BD，

此时，点B的横坐标为-1，点D的横坐标为0，

设点C的横坐标为，

∴，

解得：，

把代入函数中，得y = 1，

∴点C的坐标为（，1），

把点C的坐标为（，1）代入函数 中，

得：，

解得：；

观察图象，当时，BCBD，

故答案为：．