题目内容
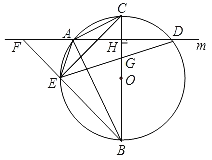
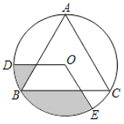
【题目】如图,等边三角形![]() 内接于
内接于![]() ,点
,点![]() 是
是![]() 上两点,且
上两点,且![]() ,若
,若![]() ,则图中阴影部分的面积为_____.
,则图中阴影部分的面积为_____.
【答案】![]()
【解析】
连接OB,OC,过点O作OH⊥BC于点H,易得:扇形OBD与扇形OCE全等,OBM OCN,进而得到:阴影部分的面积=弓形BEC的面积,根据扇形的面积公式和三角形的面积公式,即可求解.
连接OB,OC,过点O作OH⊥BC于点H,如图,
∵等边三角形![]() 内接于
内接于![]() ,点
,点![]() 是
是![]() 上两点,
上两点,
∴∠BOC=2∠BAC=2×60°=120°,∠OBC=∠OCB=30°,
∴OH=![]() ,BC=2BH=2
,BC=2BH=2![]() ,
,
∵![]() ,
,
∴∠BOC-∠BOE=∠DOE-∠BOE,即:∠BOD=∠COE,
∴扇形OBD与扇形OCE全等,
在OBM和OCN中,
∵ ,
,
∴OBM OCN(AAS),
∴阴影部分的面积=弓形BEC的面积=![]() ,
,
故答案是:![]() .
.

【题目】为了迎接疫情彻底结束后的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表
运动鞋价格 | 甲 | 乙 |
进价(元/双) |
|
|
售价(元/双) |
|
|
已知:用![]() 元购进甲种运动鞋的数量与用
元购进甲种运动鞋的数量与用![]() 元购进乙种运动鞋的数量相同.
元购进乙种运动鞋的数量相同.
![]() 求
求![]() 的值;
的值;
![]() 要使购进的甲、乙两种运动鞋共
要使购进的甲、乙两种运动鞋共![]() 双的总利润(利润
双的总利润(利润![]() 售价
售价![]() 进价)不少于
进价)不少于![]() 元,且甲种运动鞋的数量不超过
元,且甲种运动鞋的数量不超过![]() 双,问该专卖店共有几种进货方案;
双,问该专卖店共有几种进货方案;
![]() 在
在![]() 的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠
的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠![]() 元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
【题目】(2018郑州模拟)冬季即将来临,某电器超市销售每台进价分别为300元、255元的A,B两种型号的电热扇,下表是近两周的销售情况:
销售时段 | |||
销售数量 | |||
A种型号 | B种型号 | 销售收入 | |
第一周 | 2台 | 3台 | 1695元 |
第二周 | 5台 | 6台 | 3765元 |
(进价、售价均保持不变,利润![]() 销售收入
销售收入![]() 进货成本)
进货成本)
(1)分别求出A,B两种型号电热扇的销售单价;
(2)若超市准备用不超过8100元的金额再采购这两种型号的电热扇共30台,求A种型号的电热扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电热扇能否实现利润为2100元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【题目】事业单位人员编制连进必考,现一事业单位需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方而进行量化考核.甲、乙、丙各项得分如下表:
笔试 | 面试 | 体能 | |
甲 | 84 | 80 | 88 |
乙 | 94 | 92 | 69 |
丙 | 81 | 84 | 78 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;
(2)该单位规定:笔试、面试、体能分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.