题目内容
【题目】如图,直线y= ![]() x+
x+ ![]() 与两坐标轴分别交于A、B两点.
与两坐标轴分别交于A、B两点. 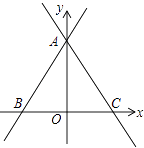
(1)求∠ABO的度数;
(2)过A的直线l交x轴半轴于C,AB=AC,求直线l的函数解析式.
【答案】
(1)解:对于直线y= ![]() x+
x+ ![]() ,
,
令x=0,则y= ![]() ,
,
令y=0,则x=﹣1,
故点A的坐标为(0, ![]() ),点B的坐标为(﹣1,0),
),点B的坐标为(﹣1,0),
则AO= ![]() ,BO=1,
,BO=1,
在Rt△ABO中,
∵tan∠ABO= ![]() =
= ![]() ,
,
∴∠ABO=60°
(2)解:在△ABC中,
∵AB=AC,AO⊥BC,
∴AO为BC的中垂线,
即BO=CO,
则C点的坐标为(1,0),
设直线l的解析式为:y=kx+b(k,b为常数),
则 ![]() ,
,
解得: ![]() ,
,
即函数解析式为:y=﹣ ![]() x+
x+ ![]()
【解析】(1)根据函数解析式求出点A、B的坐标,然后在Rt△ABO中,利用三角函数求出tan∠ABO的值,继而可求出∠ABO的度数;(2)根据题意可得,AB=AC,AO⊥BC,可得AO为BC的中垂线,根据点B的坐标,得出点C的坐标,然后利用待定系数法求出直线l的函数解析式.本题考查了待定系数法求一次函数解析式,涉及了的知识点有:待定系数法确定一次函数解析式,一次函数与坐标轴的交点,坐标与图形性质,熟练掌握待定系数法是解答本题的关键.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.

 天天练口算系列答案
天天练口算系列答案【题目】某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
各年级学生成绩统计表 | 优秀 | 良好 | 合格 | 不合格 |
七年级 | a | 20 | 24 | 8 |
八年级 | 29 | 13 | 13 | 5 |
九年级 | 24 | b | 14 | 7 |
根据以上信息解决下列问题:
(1)在统计表中,a的值为 , b的值为;
(2)在扇形统计图中,八年级所对应的扇形圆心角为度;
(3)若该校三个年级共有2000名学生参加考试,试估计该校学生体育成绩不合格的人数.
【题目】二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;
2)当 ![]() 时,y<0;
时,y<0;
3)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧.则其中正确结论的个数是( )
A.3
B.2
C.1
D.0




