Question

【题目】在中，，是边上的一点（不与点重合），边上点在点的右边且，点关于直线的对称点为，连接．

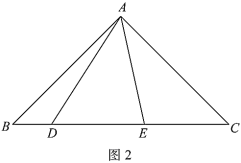
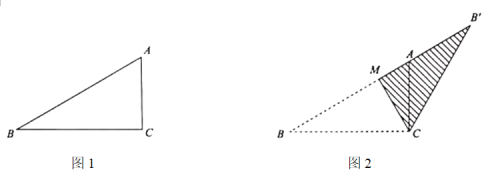
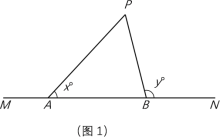
（1）如图1，

①依题意补全图1；

②求证：；

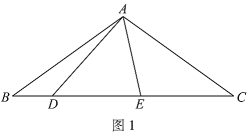
（2）如图2，，用等式表示线段，，之间的数量关系，并证明．

Answer 1

【答案】（1）①依题意补全图形，见解析；②见解析；（2）线段之间的数量关系是．证明见解析．

【解析】

（1）①根据要求画出图形即可解决；②：连接，根据对称可求出，即可得出结果；

（2）连接，由（1）②，可得，在中，由勾股定理，得，即可得到结果．

（1）①依题意补全图形，如图1．

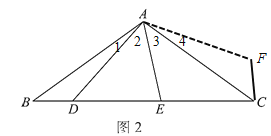
②证明：连接，如图2．

，

．

点F与点D关于直线对称，

，．

．

又，

．

．

（2）线段之间的数量关系是．

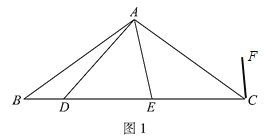
证明：连接，如图3．

，

．

由（1）②，可得．

在中，由勾股定理，得．

．