题目内容
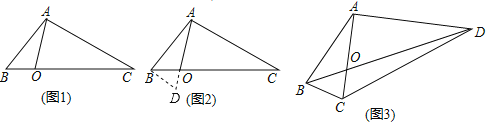
【题目】如图1,在三角形纸板![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的一个点(不与点
上的一个点(不与点![]() 重合),沿
重合),沿![]() 折叠纸板,点
折叠纸板,点![]() 的对应点是点
的对应点是点![]() .
.
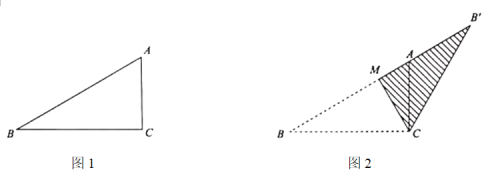
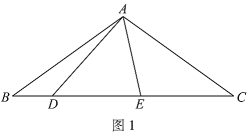
(1)如图2,当点![]() 在射线
在射线![]() 上时,
上时,![]() ________°.
________°.
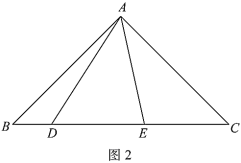
(2)若![]() ,且点
,且点![]() 不在直线
不在直线![]() 右侧,则点
右侧,则点![]() 到
到![]() 的距离是__________
的距离是__________![]() .
.
【答案】60 ![]()
【解析】
(1)解直角三角形ABC求出∠BAC=60°,得出∠B=30°,由折叠得∠BMC=90°,可得∠BCM;
(2)由折叠得![]() ,∠NCM=∠ACM=45°,根据平角的性质可求得∠BMC=105°,过M作
,∠NCM=∠ACM=45°,根据平角的性质可求得∠BMC=105°,过M作![]() 交BC于点N,得MN=NC,设
交BC于点N,得MN=NC,设![]() ,则
,则![]() ,解Rt△BMN可得BN,根据
,解Rt△BMN可得BN,根据![]() 可得结论
可得结论
(1)如图1,
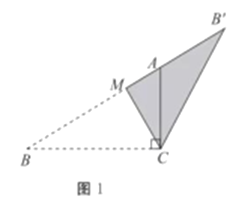
∵在Rt△ABC中,![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∵∠ACB=90°,
∴![]()
当点![]() 在射线
在射线![]() 上时,点
上时,点![]() 是
是![]() 的中点,
的中点,
∴![]() ,即
,即![]()
∴![]() ;
;
故答案为:60;
(2)如图2,
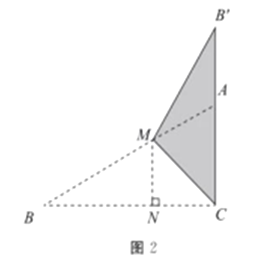
当![]() 时,由折叠得,
时,由折叠得,![]()
设![]() ,
,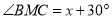
∴![]()
![]() ,
,![]()
∴∠BMC=105°,
过M作![]() 交BC于点N,由折叠得,∠NCM=∠ACM=45°
交BC于点N,由折叠得,∠NCM=∠ACM=45°
∴MN=NC
设![]() cm,则
cm,则![]() cm,
cm,
在Rt△BMN中,∠B=30°,
∴BN=![]()
∴BC=![]() +y=
+y=![]() cm
cm
解得,![]() ,即
,即![]()
∴点M到BC的距离是![]() .
.
故答案为:![]()

 中考解读考点精练系列答案
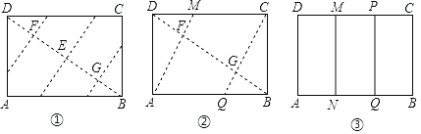
中考解读考点精练系列答案【题目】如图,已知矩形纸片ABCD,怎样折叠,能使边AB被三等分?
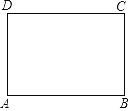
以下是小红的研究过程.
思考过程 | 要使边AB被三等分,若从边DC上考虑,就是要折出DM= 也就是要折出DM= 当DB、AM相交于F时,即要折出对角线上的DF= |
折叠方法和示意图 | ①折出DB;对折纸片,使D、B重合,得到的折痕与DB相交于点E;继续折叠纸片,使D、B与E重合,得到的折痕与DB分别相交于点F、G; ②折出AF、CG,分别交边CD、AB于M、Q; ③过M折纸片,使D落在MC上,得到折痕MN,则边AB被N、Q三等分.
|
(1)整理小红的研究过程,说明AN=NQ=QB;
(2)用一种与小红不同的方法折叠,使边AB被三等分.(需简述折叠方法并画出示意图)