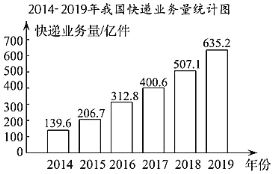
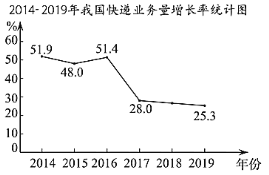
题目内容
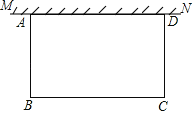
【题目】如图,在足够大的空地上有一段长为a(a≥50)米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
【答案】(1)AD的长为90m或者10m;(2)矩形菜园面积S的最大值为1250m2.
【解析】
(1)设AB=xm,则BC=(100﹣2x)m,由矩形面积公式可得x(100﹣2x)=450,解之即可解答:
(2)设AD=bm,利用矩形面积公式得矩形菜园面积S=![]() ,配方得
,配方得![]() ,根据二次函数的性质即可求得S的最大值.
,根据二次函数的性质即可求得S的最大值.
(1)设AB=xm,则BC=(100﹣2x)m,
根据题意得x(100﹣2x)=450,解得x1=5,x2=45,
当x=5时,100﹣2x=90,
当x=45时,100﹣2x=10;
答:AD的长为90m或10m;
(2)设AD=bm,
∴矩形菜园面积![]()
∵a≥50,
则b=50时,S有最大值,最大值为1250m2.

练习册系列答案
相关题目
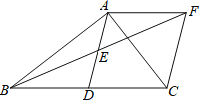
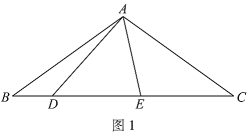
【题目】在![]() 中,
中,![]() ,
,![]() ,在图中按下列步骤进行尺规作图:
,在图中按下列步骤进行尺规作图:
① | 以 |
② | 分别以 |
③ | 画射线 |
下列说法错误的是( )
A.![]() B.
B.![]()
C.![]() D.若
D.若![]() ,则
,则![]()