Question

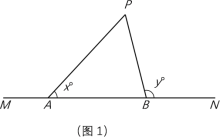
【题目】如图1，点A、B在直线MN上（A在B的左侧），点P是直线MN上方一点．若∠PAN＝x°，∠PBN＝y°，记< x，y >为P的双角坐标．例如，若△PAB是等边三角形，则点P的双角坐标为< 60，120 >．

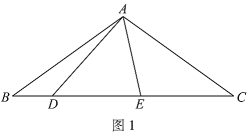
（1）如图2，若AB＝22 cm，P＜26.6，58＞，求△PAB的面积；

（参考数据：tan26.6°≈0.50，tan58°≈1.60．）

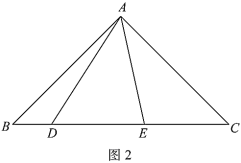
（2）在图3中用直尺和圆规作出点P < x，y >，其中y＝2x且y＝x＋30．（保留作图痕迹）

Answer 1

【答案】（1）S△PAB＝176 cm2；（2）见解析．

【解析】

（1）过P作PC⊥AB，垂足为C，则∠PCA＝90°，利用三角函数求解即可；

（2）通过y＝2x且y＝x＋30，得到x=30，y=60，可通过作等边三角形的方法作出点P．

（1）解：过P作PC⊥AB，垂足为C，则∠PCA＝90°．

在Rt△PBC中，∠PBC＝58°，

∵ tan58°＝，

∴ BC＝，

在Rt△PAC中，∠PAC＝26.6°，

∵ tan26.6°＝，

∴ AC＝，

∵ AB＝AC－BC，

∴ －＝22．

解得PC≈16 cm．

∴ S△PAB＝×22×16＝176 cm2．

（2）∵y＝2x且y＝x＋30，

∴2x＝x＋30，

即x=30，y=60，

以B为圆心AB长为半径画弧，再以A为圆心AB长为半径画弧交之前的弧于点O，然后以O为圆心AB长为半径画弧，即可得到点P，

如图，点P即为所求．