��Ŀ����
����Ŀ��������ͼ�ν�����������Ӧ��ʮ�ֹ㷺���ر�����Щ�����Ժ�ǿ����Ŀ��������ܷ�����Ŀ���������ļ������壬����ͨ���Ĵ�������ȥ˼�������������������룬�������֣���ʱ�������ת��˼ά��������Ŀ�������ļ���������ͨ�������ʺϵļ���ͼ�Σ�����õ��°빦����Ч���������������ʵ����
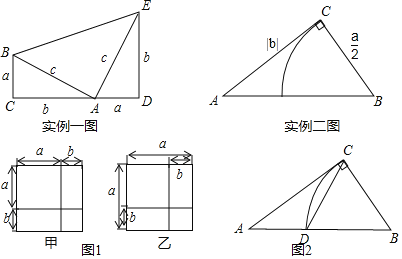
ʵ��һ��1876�꣬������ͳ٤�Ƕ�������ʵ��һͼ֤���˹��ɶ�������S�ı���ABCD=S��ABC+S��ADE+S��ABE�ã�![]() ��a+b��2=2��
��a+b��2=2��![]() ab+
ab+![]() c2������ã�a2+b2=c2��
c2������ã�a2+b2=c2��
ʵ������ŷ����õġ�����ԭ�������أ�����x�ķ���x2+ax=b2��ͼ�ⷨ�ǣ���Rt��ABC��ʹ��ACB=90����BC=![]() ��AC=|b|������б��AB�Ͻ�ȡBD=
��AC=|b|������б��AB�Ͻ�ȡBD=![]() ����AD�ij����Ǹ÷��̵�һ����������ʵ����ͼ����
����AD�ij����Ǹ÷��̵�һ����������ʵ����ͼ����
����������Ķ����ϻش���������⣺
��1����ͼ1��������ͼ��������ĵ�����ϵ��д����ͼҪ֤������ѧ��ʽ��______����ͼҪ֤������ѧ��ʽ��______�����ֵ���ѧ˼����______��
��2����ͼ2����2��-8�ǹ���x�ķ���x2+ax=b2��������������ʵ�����ķ�ʽ����Rt��ABC������CD����CD�ij���
��3����x��y��z��Ϊ��������x2+y2=z2�����ù���ͼ�εķ�����![]() �����ֵ��
�����ֵ��
���𰸡���1����ȫƽ����ʽ��ƽ���ʽ�����ν�ϵ�˼�루2��![]() ��3��
��3��![]()
��������
��1�����������������⼴�ɣ�
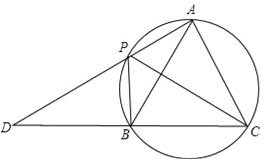
��2����ͼ2�У���CH��AB��H�������⣬AD=2��BC=BD=3��AC=4��������������CH��BH��DH���ɽ�����⣻
��3����ͼ3�У���4��ȫ�ȵ�ֱ�������Σ�ֱ�DZ߷ֱ�Ϊx��y��б��Ϊz����ƴ��ͼ�����Σ���x+y�Ƕ�ֵʱ��z��С��ʱ��![]() ��ֵ��С����֪��С�����εĶ����Ǵ������ε��е�ʱ��z��ֵ��С����ʱx=y��z=
��ֵ��С����֪��С�����εĶ����Ǵ������ε��е�ʱ��z��ֵ��С����ʱx=y��z=![]() x���ɴ˼��ɽ�����⣮
x���ɴ˼��ɽ�����⣮
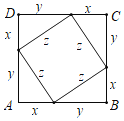
��1����ͼ1�У�ͼ�״������ε����=��a+b��2=a2+2ab+b2��
ͼ���д������ε����=a2=��a-b��2+b2+2b��a-b����
��a2-b2=��a-b����a-b+2b��=��a+b����a-b����
��ͼҪ֤������ѧ��ʽ����ȫƽ����ʽ����ͼҪ֤������ѧ��ʽ��ƽ���ʽ�����ֵ���ѧ˼�������ν�ϵ�˼�룮
�ʴ�Ϊ����ȫƽ����ʽ��ƽ���ʽ�����ν�ϵ�˼�룮
��2����ͼ2�У���CH��AB��H��
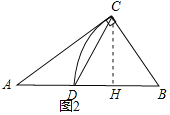
�����⣬AD=2��BC=BD=3��AC=4��
��![]() ACBC=
ACBC=![]() ABCH��
ABCH��
��CH=![]() ��
��
��BH=![]() ��
��
��DH=BD-BH=![]() ��
��
��CD=![]() ��
��
��3����ͼ3�У���4��ȫ�ȵ�ֱ�������Σ�ֱ�DZ߷ֱ�Ϊx��y��б��Ϊz����ƴ��ͼ�����Σ�
��x+y�Ƕ�ֵʱ��z��С��ʱ��![]() ��ֵ��С��
��ֵ��С��
��֪��С�����εĶ����Ǵ������ε��е�ʱ��z��ֵ��С����ʱx=y��z=![]() x��
x��
��![]() ���ֵ=
���ֵ=![]() ��
��