题目内容
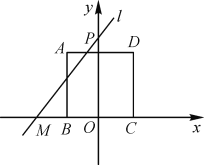
【题目】如图,正方形ABCD的边长为2,BC边在x轴上,BC的中点与原点O重合,过定点M(-2,0)与动点P(0,t)的直线MP记作l.
(1)若l的解析式为y=2x+4,判断此时点A是否在直线l上,并说明理由;
(2)当直线l与AD边有公共点时,求t的取值范围.
【答案】(1)点A在直线l上,理由见解析;(2)![]() ≤t≤4.
≤t≤4.
【解析】
(1)由题意得点B、A坐标,把点A的横坐标x=-1代入解析式y=2x+4得出y的值,即可得出点A在直线l上;
(2)当直线l经过点D时,设l的解析式代入数值解出即可
(1)此时点A在直线l上.
∵BC=AB=2,点O为BC中点,
∴点B(-1,0),A(-1,2).
把点A的横坐标x=-1代入解析式y=2x+4,得
y=2,等于点A的纵坐标2,
∴此时点A在直线l上.
(2)由题意可得,点D(1,2),及点M(-2,0),
当直线l经过点D时,设l的解析式为y=kx+t(k≠0),
∴![]() 解得
解得![]()
由(1)知,当直线l经过点A时,t=4.
∴当直线l与AD边有公共点时,t的取值范围是![]() ≤t≤4.
≤t≤4.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目