题目内容
【题目】数学活动课上,老师提出了一个问题:
我们知道,三角形的一个外角等于和它不相邻的两个内角的和,那么三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系?
(1)独立思考,请你完成老师提出的问题:
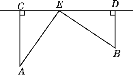
如图所示,已知∠DBC和∠BCE分别为△ABC的两个外角,试探究∠A和∠DBC,∠BCE之间的数量关系.

解:
⑵合作交流,“创新小组”受此问题的启发:分别作外角∠CBD和∠BCE的平分线BF和CF,交于点F(如图所示),那么∠A与∠F之间有何数量关系?请写出解答过程.

【答案】(1)∠DBC+∠BCE-∠A=180(2)![]() ∠A+∠F=90
∠A+∠F=90
【解析】
(1)根据三角形的一个外角等于和它不相邻的两个内角的和,三角形内角和定理计算即可.
(2)根据角平分线可知∠FBC+∠FCB=![]() (∠DBC+∠BCE,)再根据三角形内角和定理,结合(1)即可解答.
(∠DBC+∠BCE,)再根据三角形内角和定理,结合(1)即可解答.
⑴∠DBC+∠BCE-∠A=180.
∠DBC+∠BCE
=∠ABC+∠A+∠ACB+∠A
=180°+∠A
即∠DBC+∠BCE-∠A=180.
(2)![]() ∠A+∠F=90°
∠A+∠F=90°
∵BF和CF分别平分∠CBD和∠BCE,
∴∠CBF=![]() ∠CBD,∠BCF=
∠CBD,∠BCF=![]() ∠BCE.
∠BCE.
∴∠CBF+∠BCF=![]() (∠CBD+∠BCE).
(∠CBD+∠BCE).
∵∠CBF+∠BCF=180-∠F,∠DBC+∠BCE=180+∠A.
∴180-∠F =![]() (∠CBD+∠BCE)=
(∠CBD+∠BCE)=![]() (180+∠A)
(180+∠A)
∴![]() ∠A+∠F=90.
∠A+∠F=90.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目