题目内容
【题目】如图,四边形ABCD是矩形,![]() ,
,![]() ,点P是对角线AC上的动点
,点P是对角线AC上的动点![]() 不与点A,C重合
不与点A,C重合![]() ,连接PD,作
,连接PD,作![]() 交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.
交射线BC于点E,以线段PD,PE为邻边作矩形PEFD.

![]() 线段PD的最小值为______;
线段PD的最小值为______;
![]() 求证:
求证:![]() ,并求矩形PEFD面积的最小值;
,并求矩形PEFD面积的最小值;
![]() 是否存在这样的点P,使得
是否存在这样的点P,使得![]() 是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由.
是等腰三角形?若存在,请求出PE的长;若不存在,请说明理由.
【答案】(1)![]() ;(2)证明见解析;(3) PE的长为
;(2)证明见解析;(3) PE的长为![]() 或
或![]() .
.
【解析】
![]() 如图1中,根据垂线段最短可知,当
如图1中,根据垂线段最短可知,当![]() 时,DP的值最小
时,DP的值最小![]() 利用面积法即可解决问题;
利用面积法即可解决问题;
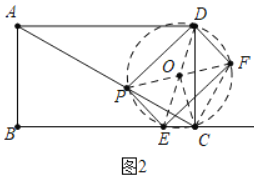
![]() 如图2中,连接DE、PF交于点O,连接FC,
如图2中,连接DE、PF交于点O,连接FC,![]() 首先证明D、P、E、C、F五点共圆,由
首先证明D、P、E、C、F五点共圆,由![]() ∽
∽![]() ,推出
,推出![]() ,即可解决问题;
,即可解决问题;
![]() 分两种情形:点E在线段BC上,点E在线段BC的延长线上,分别求解即可解决问题;
分两种情形:点E在线段BC上,点E在线段BC的延长线上,分别求解即可解决问题;
![]() 解:如图1中,根据垂线段最短可知,当
解:如图1中,根据垂线段最短可知,当![]() 时,DP的值最小.
时,DP的值最小.
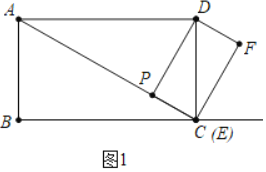
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故答案为![]() .
.
![]() 证明:如图2中,连接DE、PF交于点O,连接FC,OC.
证明:如图2中,连接DE、PF交于点O,连接FC,OC.
![]() 四边形DPEF是矩形,
四边形DPEF是矩形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 、P、E、C、F五点共圆,
、P、E、C、F五点共圆,
![]() 是直径,
是直径,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
∴S矩形PEFD=PE·PD=![]() PD2.
PD2.
∵PD的最小值是![]() ,
,
∴矩形PEFD面积的最小值是=![]() ×(
×(![]() )2=
)2=![]() .
.
![]() 解:如图3中,设AC交DE于H.
解:如图3中,设AC交DE于H.
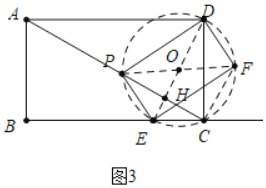
当![]() 时,易证
时,易证![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
如图4中,
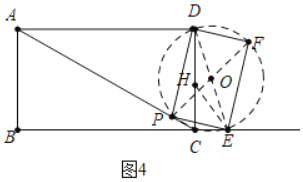
当![]() 时,
时,![]() ,
,
![]() ,
,
在CD上取一点H,速度![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
综上所述,PE的长为![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目