ЬтФПФкШн
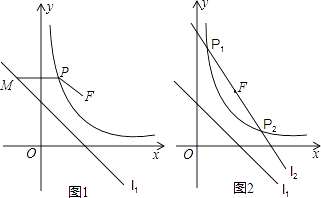
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌвбжЊжБЯп![]() ЃЌдкжБЯп
ЃЌдкжБЯп![]() ЩЯШЁ
ЩЯШЁ![]() СНЕуЃЌ
СНЕуЃЌ![]() ЮЊжБЯп
ЮЊжБЯп![]() ЩЯЕФСНЕуЃЌЮоТлЕу
ЩЯЕФСНЕуЃЌЮоТлЕу![]() вЦЖЏЕНШЮКЮЮЛжУЖМгаЃК
вЦЖЏЕНШЮКЮЮЛжУЖМгаЃК![]() ____________
____________![]() ЃЈЬюЁА>ЁБЁЂЁА<ЁБЛђЁА=ЁБЃЉ
ЃЈЬюЁА>ЁБЁЂЁА<ЁБЛђЁА=ЁБЃЉ
ЃЈ2ЃЉШчЭМ2ЃЌдквЛПщЬнаЮЬяЕиЩЯЗжБ№вЊжжжВДѓЖЙЃЈПеАзВПЗжЃЉКЭжЅТщЃЈвѕгАВПЗжЃЉЃЌШєЯыАбжжжВДѓЖЙЕФСНПщЕиИФЮЊвЛПщЕиЃЌЧвЪЙЗжБ№жжжВСНжжжВЮяЕФУцЛ§ВЛБфЃЌЧыЮЪгІИУдѕУДИФНјФиЃПаДГіЩшМЦЗНАИЃЌВЂдкЭМжаЛГіЯргІЭМаЮВЂМђЪіРэгЩЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌЭѕвЏвЏКЭРювЏвЏСНМвЬяЕиаЮГЩСЫЫФБпаЮ![]() ЃЌжаМфгаЬѕЗжНчаЁТЗЃЈЭМжаелЯп
ЃЌжаМфгаЬѕЗжНчаЁТЗЃЈЭМжаелЯп![]() ЃЉЃЌзѓБпЧјгђЮЊЭѕвЏвЏЕФЃЌгвБпЧјгђЮЊРювЏвЏЕФЁЃЯждкзМБИАбСНМвЬяЕижЎМфЕФаЁТЗИФЮЊжБТЗЃЌЧыФугУгаЙиЕФМИКЮжЊЪЖЃЌАДвЊЧѓЩшМЦГіаоТЗЗНАИЃЌВЂдкЭМжаЛГіЯргІЕФЭМаЮЃЌЫЕУїЗНАИЩшМЦРэгЩЁЃЃЈВЛМЦЗжНчаЁТЗгыжБТЗЕФеМЕиУцЛ§ЃЉЃЎ
ЃЉЃЌзѓБпЧјгђЮЊЭѕвЏвЏЕФЃЌгвБпЧјгђЮЊРювЏвЏЕФЁЃЯждкзМБИАбСНМвЬяЕижЎМфЕФаЁТЗИФЮЊжБТЗЃЌЧыФугУгаЙиЕФМИКЮжЊЪЖЃЌАДвЊЧѓЩшМЦГіаоТЗЗНАИЃЌВЂдкЭМжаЛГіЯргІЕФЭМаЮЃЌЫЕУїЗНАИЩшМЦРэгЩЁЃЃЈВЛМЦЗжНчаЁТЗгыжБТЗЕФеМЕиУцЛ§ЃЉЃЎ



ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉМћНтЮі
ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦНааЯпМфЕФОрРыДІДІЯрЕШЃЌЫљвдЮоТлЕу![]() дкmЩЯвЦЖЏЕНКЮЮЛжУЃЌзмга
дкmЩЯвЦЖЏЕНКЮЮЛжУЃЌзмга![]() гы
гы![]() ЭЌЕзЕШИпЃЌвђДЫЫќУЧЕФУцЛ§ЯрЕШЃЛ
ЭЌЕзЕШИпЃЌвђДЫЫќУЧЕФУцЛ§ЯрЕШЃЛ
ЃЈ2ЃЉРћгУЭЌЕзЕШИпЕФШ§НЧаЮЕФУцЛ§ЯрЕШМДПЩЧѓЕУЩшМЦЗНАИЃЛ
ЃЈ3ЃЉСЌНс![]() ЃЌЙ§
ЃЌЙ§![]() Еузї
Еузї![]() ЕФЦНааЯп
ЕФЦНааЯп![]() ЃЌСЌНс
ЃЌСЌНс![]() Лђ
Лђ![]() ЃЌдђ
ЃЌдђ![]() Лђ
Лђ![]() МДЮЊЫљаожБТЗЃЎ
МДЮЊЫљаожБТЗЃЎ
ЃЈ1ЃЉЁп![]() гы
гы![]() гаЙВЭЌЕФБпABЃЌ
гаЙВЭЌЕФБпABЃЌ
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() гы
гы![]() ЕФИпЯрЕШЃЌМД
ЕФИпЯрЕШЃЌМД![]() гы
гы![]() ЭЌЕзЕШИпЃЌ
ЭЌЕзЕШИпЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК=ЃЛ
ЃЈ2ЃЉЗНЗЈвЛЃК
СЌНс![]() ЃЌНЋ
ЃЌНЋ![]() ЕФЧјгђгУгкжжжВДѓЖЙЃЌ
ЕФЧјгђгУгкжжжВДѓЖЙЃЌ![]() ЕФЧјгђгУгкжжжВжЅТщЃЌРэгЩШчЯТЃК
ЕФЧјгђгУгкжжжВжЅТщЃЌРэгЩШчЯТЃК
дкЬнаЮABCDжа,![]() ЃЌ
ЃЌ
дђ![]() гы
гы![]() ЭЌЕзЕШИпЃЌ
ЭЌЕзЕШИпЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
гжгЩ![]() ПЩжЊ
ПЩжЊ![]() гы
гы![]() ЭЌЕзЕШИпЃЌ
ЭЌЕзЕШИпЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрИУЩшМЦЗНАИАбжжжВДѓЖЙЕФСНПщЕиИФЮЊвЛПщЕиЃЌЧвЪЙЗжБ№жжжВСНжжжВЮяЕФУцЛ§ВЛБфЃЛ
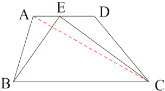
ЗНЗЈЖў
СЌНс![]() ЃЌНЋ
ЃЌНЋ![]() ЕФЧјгђгУгкжжжВДѓЖЙЃЌ
ЕФЧјгђгУгкжжжВДѓЖЙЃЌ![]() ЕФЧјгђгУгкжжжВжЅТщЃЌРэгЩШчЯТЃК
ЕФЧјгђгУгкжжжВжЅТщЃЌРэгЩШчЯТЃК
дкЬнаЮABCDжа,![]() ЃЌ
ЃЌ
дђ![]() гы
гы![]() ЭЌЕзЕШИпЃЌ
ЭЌЕзЕШИпЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
гжгЩ![]() ПЩжЊ
ПЩжЊ![]() гы
гы![]() ЭЌЕзЕШИпЃЌ
ЭЌЕзЕШИпЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрИУЩшМЦЗНАИАбжжжВДѓЖЙЕФСНПщЕиИФЮЊвЛПщЕиЃЌЧвЪЙЗжБ№жжжВСНжжжВЮяЕФУцЛ§ВЛБфЃЛ

ЃЈ3ЃЉЗНЗЈвЛ
СЌНс![]() ЃЌЙ§
ЃЌЙ§![]() Еузї
Еузї![]() ЕФЦНааЯп
ЕФЦНааЯп![]() ЃКСЌНс
ЃКСЌНс![]() ЃЌ
ЃЌ![]() МДЮЊЫљаожБТЗЃЎ
МДЮЊЫљаожБТЗЃЎ
НЋЫФБпаЮ![]() ЕФЧјгђЗжИјЭѕвЏвЏЃЌЫФБпаЮ
ЕФЧјгђЗжИјЭѕвЏвЏЃЌЫФБпаЮ![]() ЕФЧјгђЗжИјРювЏвЏЃЌРэгЩШчЯТЃК
ЕФЧјгђЗжИјРювЏвЏЃЌРэгЩШчЯТЃК
Ёп![]() ЃЌдђ
ЃЌдђ![]() гы
гы![]() ЭЌЕзЕШИпЃЌ
ЭЌЕзЕШИпЃЌ
Ёр![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
гжгЩ![]() ПЩжЊ
ПЩжЊ![]() гы
гы![]() ЭЌЕзЕШИпЃЌ
ЭЌЕзЕШИпЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ТњзуаоТЗЗНАИЃЛ
ТњзуаоТЗЗНАИЃЛ
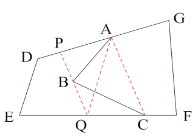
ЗНЗЈЖўЃК
СЌНс![]() ЃЌЙ§
ЃЌЙ§![]() Еузї
Еузї![]() ЕФЦНааЯп
ЕФЦНааЯп![]() ЃКСЌНс
ЃКСЌНс![]() ЃЌ
ЃЌ![]() МДЮЊЫљаожБТЗЃЎ
МДЮЊЫљаожБТЗЃЎ
НЋЫФБпаЮ![]() ЕФЧјгђЗжИјЭѕвЏвЏЃЌЫФБпаЮ
ЕФЧјгђЗжИјЭѕвЏвЏЃЌЫФБпаЮ![]() ЕФЧјгђЗжИјРювЏвЏЃЌРэгЩШчЯТЃК
ЕФЧјгђЗжИјРювЏвЏЃЌРэгЩШчЯТЃК
Ёп![]() ЃЌдђ
ЃЌдђ![]() гы
гы![]() ЭЌЕзЕШИпЃЌ
ЭЌЕзЕШИпЃЌ
Ёр![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
гжгЩ![]() ПЩжЊ
ПЩжЊ![]() гы
гы![]() ЭЌЕзЕШИпЃЌ
ЭЌЕзЕШИпЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ТњзуаоТЗЗНАИЃЎ
ТњзуаоТЗЗНАИЃЎ
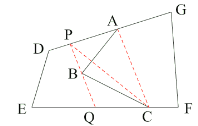

ЁОЬтФПЁПОХЃЈ1ЃЉАрЪ§бЇаЫШЄаЁзщОЙ§ЪаГЁЕїВщЃЌећРэГіФГжжЩЬЦЗдкЕкxЃЈ1ЁмxЁм90ЃЉЬьЕФЪлМлгыЯњСПЕФЯрЙиаХЯЂШчЯТБэЃК
ЪБМфxЃЈЬьЃЉ | 1ЁмxЃМ50 | 50ЁмxЁм90 |
ЪлМлЃЈдЊ/МўЃЉ | x+40 | 90 |
УПЬьЯњСПЃЈМўЃЉ | 200Љ2x | |
вбжЊИУЩЬЦЗЕФНјМлЮЊУПМў30дЊЃЌЩшЯњЪлИУЩЬЦЗЕФУПЬьРћШѓЮЊyдЊЃЎ
ЃЈ1ЃЉЧѓГіyгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЮЪЯњЪлИУЩЬЦЗЕкМИЬьЪБЃЌЕБЬьЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉИУЩЬЦЗдкЯњЪлЙ§ГЬжаЃЌЙВгаЖрЩйЬьУПЬьЯњЪлРћШѓВЛЕЭгк4800дЊЃПЧыжБНгаДГіНсЙћЃЎ