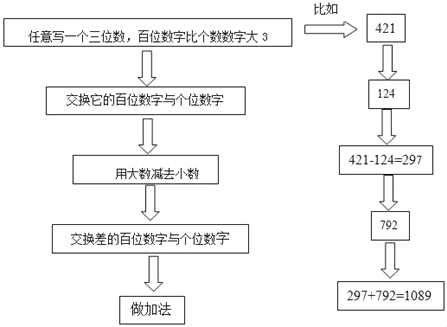
��Ŀ����
����Ŀ������Ҫ��ش����⣺
��1����������⡿
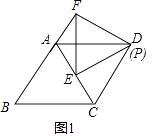
��֪������ABCD�ı䳤Ϊ4����ADC=60�㣬��PEFΪ�ȱ������Σ�����P���D�غϣ���E�ڶԽ���AC��ʱ����ͼ1��ʾ������AE+AF��ֵ��
��2�������̽����
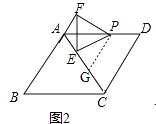
������������У�����ѵ�P��DA�����ƶ���ʹPD=1�������������䣨��ͼ2�������ܷ���AE+AF��ֵ�Ƕ��٣���ֱ��д����Ľ��ۣ�
��3������չǨ�ơ�
��ԭ�����У�����P���߶�DA���ӳ����ϣ���E��CA���ӳ�����ʱ����ͼ3������AP=m�����߶�AE��AF�ij���m��������������ϵ����˵�����ɣ�
���𰸡�
��1���⣺��ͼ1��
 ��
��
���ı���ABCD�����Σ�
��PA=PC��
�ߡ�ADC=60�㣬
���ACD�ǵȱ������Σ�
��AC=AD=4��
�֡ߡ�PEFΪ�ȱ������Σ�
���ADC=��EPF=60�㣬
���APF=��CPE��
�ڡ�APF�͡�CPE�У�
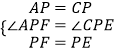
���APF�ա�CPE��
��CE=AF��
��AE+AF=AE+CE=AC=4��
��AE+AF��ֵ��4��
��2���⣺��ͼ2����G��AC�ϵ�һ�㣬������CG=PD=1��
 ��
��
��CG=PD��AC=AD��
��AG=AP��
�� ![]() ��
��
��GP��CD��
���GPA=��CDA=60�㣬
�֡�EPF=60�㣬
���APF=��GPE��
�ڡ�APF�͡�GPE�У�
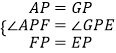
���APF�ա�GPE��
��GE=AF��
��AE+AF=AE+GE=AG=AC��CG=4��1=3��
��AE+AF��ֵ��3
��3���⣺��ͼ3����PH��CD��CE�ڵ�H��
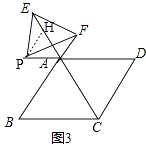 ��
��
�ɣ�1�����ɵá�ACD�ǵȱ������Σ�
��PH��CD��
���AHP�ס�ACD��
���AHP�ǵȱ������Σ�
��PA=PH����APH=��EPF=60�㣬
���FPA=��EPH��
�ڡ�APF�͡�HPE�У�
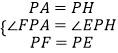
���APF�ա�HPE��
��AF=HE��
�֡�PA=AH��
��AE=PA+AF��
��AE��AF=m��
����������1�������жϳ���ACD�ǵȱ������Σ������жϳ�AC=AD=4��Ȼ�����ȫ���������ж��ķ������жϳ���APF�ա�CPE�������жϳ�CE=AF���ݴ����AE+AF��ֵ�Ƕ��ټ��ɣ���2������ȡAC�ϵĵ�G��ʹ��CG=PD=1���жϳ�GP��CD�������жϳ���APF=��GPE��Ȼ�����ȫ���������ж��ķ������жϳ���APF�ա�GPE�������жϳ�GE=AF���ݴ����AE+AF��ֵ�Ƕ��ټ��ɣ���3��������PH��CD��CE�ڵ�H���жϳ���AHP�ס�ACD�������жϳ���AHP�ǵȱ������Σ�Ȼ�����ȫ���������ж��ķ������жϳ���APF�ա�HPE�������жϳ�AF=HE���ٸ���PA=AH���ɵ�AE=PA+AF������AE��AF=m���ݴ˽�ɣ�
�����㾫����������Ĺؼ���������ȫ�������ε����ʵ����֪ʶ������ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ��Լ������ε����ʵ����⣬�˽����ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�룮

 ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д� ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�