Question

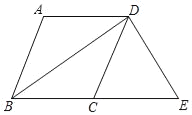
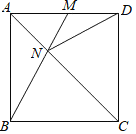
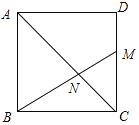
【题目】如图所示，在正方形ABCD中，AD＝6，M在AD上从A向D运动，连接BM交AC于N，连接DN．

（1）证明：无论M运动到AD上的何处，都有△ABN≌△ADN；

（2）当M运动到何处时，S△ABN＝S正方形ABCD？

（3）若M从A到D，再从D到C，在整个运动过程中，DM为多少时，△ABN是等腰三角形？

Answer 1

【答案】（1）见解析；（2）AM＝2时；（3）当DM＝0或6或12﹣6时，△ABN是等腰三角形

【解析】

（1）由正方形的性质得出AB＝AD＝BC＝6，∠BAN＝∠DAN，AD∥BC，由SAS证明△ABN≌△ADN即可；

（2）由正方形的性质得出，得出，由平行线得出△AMN∽△CBN，得出，求出；

（3）分三种情况：①若AN＝BN，此时M与D重合，DM＝0；

②若AB＝BN，此时M与重合，DM＝6；

③若AB＝AN，此时点M在DC上，由平行线得出△ABN∽△CMN，得出CM＝CN，求出，即可得出．

（1）证明：∵四边形ABD是正方形

∴AB＝AD＝BC＝6，∠BAN＝∠DAN，AD∥BC

在△ABN和△ADN中，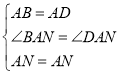

；

（2）

，即

，即

∵AM∥BC

∴△AMN∽△CBN

即当AM＝2时，；

（3）若△ABN是等腰三角形，分三种情况：

①若AN＝BN，此时M与D重合，DM＝0

②若AB＝BN，此时M与重合，DM＝6

③若AB＝AN，此时点M在DC上，如图所示：

∵AB∥CM

∴△ABN∽△CMN

∴

∴CM＝CN

综上，当DM＝0或6或时，△ABN是等腰三角形．