题目内容
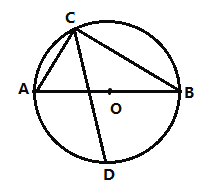
【题目】如图所示,△ABC内接于⊙O,AC是直径,D在⊙O上,且AC平分∠BCD,AE∥BC,交CD于E,F在CD的延长线上,且AE=EF.连接AF
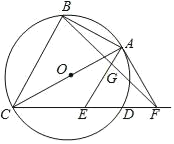
(1)求证:AF是⊙O的切线;
(2)连接BF交AE于G,若AB=12,AE=13,求AG的长.
【答案】(1)见解析;(2)AG=4.
【解析】
(1)由角平分线的性质和平行线的性质可得AE=CE=EF,可得∠CAF=90°,即可证AF是⊙O的切线;
(2)连接AD,由“AAS”可证△ABC≌△ADC,可得AB=AD=12,BC=CD,由勾股定理可求DE=5,由平行线分线段成比例可求GE=9,即可求AG的长.
解:证明:(1)∵AC平分∠BCD
∴∠ACB=∠ACD,
∵AE∥BC
∴∠ACB=∠CAE=∠ACD
∴AE=CE,且AE=EF
∴AE=CE=EF
∴△CAF是直角三角形
∴∠CAF=90°
∴AF是⊙O的切线
(2)连接AD,
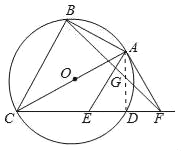
∵AC是直径
∴∠ABC=90°=∠ADC
∵∠ACB=∠ACD,AC=AC,∠ABC=∠ADC=90°
∴△ABC≌△ADC(AAS)
∴AB=AD=12,BC=CD
在Rt△AED中,DE=![]()
∵AE=CE=EF=13
∴CF=2EF,CD=BC=CE+DE=18,
∵AE∥BC
∴![]()
∴EG=9
∴AG=AE﹣EG=13﹣9=4

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目