Question

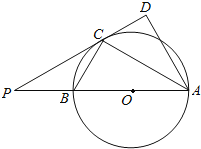
【题目】如图，AB是⊙O的直径，点C是⊙O上一点，AD⊥DC于D，且AC平分∠DAB．延长DC交AB的延长线于点P．

（1）求证：PC2＝PAPB；

（2）若3AC＝4BC，⊙O的直径为7，求线段PC的长．

Answer 1

【答案】（1）见解析；（2）PC＝12．

【解析】

（1）证明△PAC∽△PCB，可得，即可证明PC2=PAPB；

（2）若3AC=4BC，则，由（1）可求线段PC的长．

（1）∵AB是⊙O的直径，

∴∠ACB=90°．

∵AD⊥DC于D，且AC平分∠DAB，

∴∠PDA=90°，∠DAC=∠BAC．

∵∠PCA=∠PDA+∠DAC，∠PBC=∠ACB+∠BAC，

∴∠PCA=∠PBC．

∵∠BPC=∠CPA，

∴△PAC∽△PCB，

∴，

∴PC2=PAPB；

（2）∵3AC=4BC，

∴．

设PC=4k，则PB=3k，PA=3k+7，

∴(4k)2=3k(3k+7)，

∴k=3或k=0(舍去)，

∴PC=12．