题目内容
【题目】如图，BD是ABCD的对角线，AB⊥BD，BD=8cm，AD=10cm，动点P从点D出发，以5cm/s的速度沿DA运动到终点A，同时动点Q从点B出发，沿折线BD-DC运动到终点C，在BD、DC上分别以8cm/s、6cm/s的速度运动．过点Q作QM⊥AB，交射线AB于点M，连接PQ，以PQ与QM为边作□PQMN．设点P的运动时间为t（s）（t＞0），PQMN与ABCD重叠部分图形的面积为S（cm2）．
（1）AP= cm（用含t的代数式表示）．
（2）当点N落在边AB上时，求t的值．
（3）求S与t之间的函数关系式．
（4）连结NQ，当NQ与△ABD的一边平行时，直接写出t的值．
【答案】（1）10-5t；（2）t= 
；（3）见解析；（4）
秒或
秒或2秒．
【解析】
（1）先表示PD=t，可得AP=10-5t；
（2）如图1，点N落在边AB上，则AP=10-2t，PN=BQ=8t，证明△APN∽△ADB，列比例式得方程，可得t的值；
（3）分三种情况
①当0＜t≤时，如图2，过点P作PE⊥BD于点E，PQMN与ABCD重叠部分图形是PQMN，
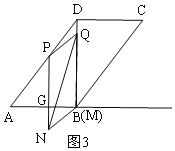
②当＜t≤1时，如图3，PQMN与ABCD重叠部分图形是四边形PQMG，
③当1＜t≤2时，如图4，PQMN与ABCD重叠部分图形是五边形PQHBG，
根据三角形和四边形面积和与差可得结论；
（4）分三种情况：①当NQ∥AD时，如图5，根据DQ=BQ=4=8t，得结论；
②当NQ∥AB时，如图6，根据PN=BQ=8t，列方程为：8t+8t=8-4t，得结论；
③如图7，当Q与C重合，P与A重合时，t=2．
（1）由题意得：PD=t，
∵AD=10，
∴AP=10-5t，
故答案为：（10-5t）；
（2）如图1，点N落在边AB上，则AP=10-2t，PN=BQ=8t，
∵PN∥BD，
∴△APN∽△ADB，
∴
，
∴
，
(105t)＝8t，
∴t＝.
（3）分三种情况：
①当0＜t≤时，如图2，过点P作PE⊥BD于点E，PQMN与ABCD重叠部分图形是PQMN，
则PE=3t．
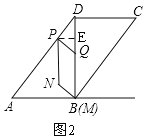
S=BQBE=3t8t=24t2；
②当＜t≤1时，如图3，PQMN与ABCD重叠部分图形是四边形PQMG，则BG=3t，
，
，
∴
；
③当1＜t≤2时，如图4，PQMN与ABCD重叠部分图形是五边形PQHBG，
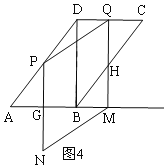
则PG=（10-5t）=8-4t，MQ=8，MG=BG+MB=6（t-1）+3t=9t-6，
，
∴
，
∴S=S梯形PQMG-S△HBM=（PG+QM）MG-BMHM，
=（9t-6）[8-4t+8]- （6t-6）（8t-8），
=-42t2+132t-72；
（4）①当NQ∥AD时，如图5，
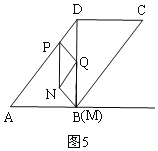
∴∠DPQ=∠PQN=∠QNB，
∵PQ=BN，∠PQD=∠NBQ，
∴△DPQ≌△QNB，
∴DQ=BQ=×8=4，
即8t=4，t=；
②当NQ∥AB时，如图6，延长PN交AB于G，则PG⊥AB，则PG=8-4t，
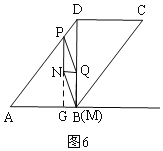
∵PN=BQ=8t，
∴8t+8t=8-4t，t=，
③如图7，当Q与C重合，P与A重合时，t=2，
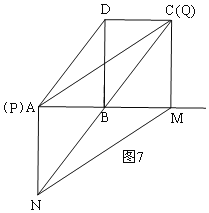
此时，CM=AN=8，B是AM的中点，
NC在直线BC上，
∴NQ∥AD，
综上所述，t的值为秒或秒或2秒．
